レイノルズのボイド

提供：kuhalaboWiki
移動： 案内, 検索

目次

概要

ボイド(Boids)は、クレイグ・レイノルズが考案・作製した人工生命シミュレーションプログラムである。名称は「鳥もどき(bird-oid)」から取られている。コンピュータ上の鳥オブジェクトに以下の三つの動作規則を与え、多数を同時に動かして群れの振る舞いをシミュレーションする。

ボイド wiki / Reynolds Boids official /

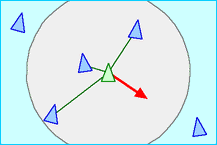
分離（Separation）
鳥は群れの鳥(Local flockmates)とぶつからないように距離をとる。

Separation.gif

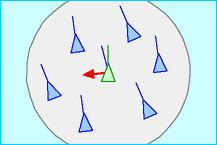
整列（Alignment）
鳥は群れの鳥(Local flockmates)と概ね同じ方向に飛ぶように速度と方向を合わせる。

Alignment.gif

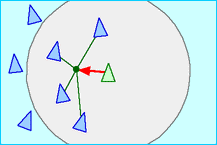
結合（Cohesion）
鳥は群れの鳥(Local flockmates)が集まっている中心方向へ向かうように方向を変える。

Cohesion.gif

驚くほど自然な動きを見せ、単純な規則を用いて群としての複雑な振る舞いを再現できる。

Processing公式サイトのソース例

Birds Algorhythm Craig Reynolds Processing official より引用(一部改変)

  • TWO_PI 3.1415...（円周率）×2のこと
  • PVectorオブジェクトの演算
    • x.normalize() ベクトルxの大きさを1にする。
    • x.mag() ベクトルxの大きさを求める。
    • x.add(y) 足し算 x+y
    • x.sub(y) 引き算 x-y
    • x.mult(y) 掛け算 x*y
    • x.div(y) 割り算 x/y
    • x.limit(y) 上限値 max(x,y)：xの上限(最大値)はy
    • dist(x,y) xとyの距離　sqrt(x*x + y*y)
  • pushMatrix(), translate(x,y);rotate(theta);beginShape();vertex();endShape();popMatrix();を使った鳥（三角形）の描画
  • クラスの設計
    • Flock 鳥の群れ：Boidオブジェクトのリスト
    • Boid 1羽の鳥
      • separate() 分離の加速度を計算
        • 距離がdesiredseparationの値より小さいと近すぎるとみなし、分離しようとする。
      • align() 整列の加速度を計算
        • 距離がneighbordistの値より小さいと近傍（群れの仲間）とみなし、整列しようとする。群れの平均速度（速さと方向）に合わせようとする。
      • cohesion() 結合の加速度を計算
        • 距離がneighbordistの値より小さいと近傍（群れの仲間）とみなし、結合しようとする。群れの中心に向かおうとする。
      • seek(PVector target) targetを追跡(seek)する加速度の計算 
Flock flock;

void setup() {
  size(800,800);
  flock = new Flock();
  // Add an initial set of boids into the system
  for (int i = 0; i < 150; i++) {
    flock.addBoid(new Boid(width/2,height/2));
  }
}

void draw() {
  background(50);
  flock.run();
}

// Add a new boid into the System
void mousePressed() {
  flock.addBoid(new Boid(mouseX,mouseY));
}

// The Flock (a list of Boid objects)
class Flock {
  ArrayList<Boid> boids; // An ArrayList for all the boids
  Flock() {
    boids = new ArrayList<Boid>(); // Initialize the ArrayList
  }
  void run() {
    for (Boid b : boids) {
      b.run(boids);  // Passing the entire list of boids to each boid individually
    }
  }
  void addBoid(Boid b) {
    boids.add(b);
  }
}

// The Boid class
class Boid {
  PVector position;
  PVector velocity;
  PVector acceleration;
  float r;           // Bird size
  float maxforce;    // Maximum steering force
  float maxspeed;    // Maximum speed

  Boid(float x, float y) {
    acceleration = new PVector(0, 0);
    float angle = random(TWO_PI);
    velocity = new PVector(cos(angle), sin(angle));
    position = new PVector(x, y);
    r = 2.0;
    maxspeed = 2;
    maxforce = 0.03;
  }

  void run(ArrayList<Boid> boids) {
    flock(boids);
    update();
    borders();
    render();
  }

  void applyForce(PVector force) {
    // We could add mass here if we want A = F / M
    acceleration.add(force);
  }

  // We accumulate a new acceleration each time based on three rules
  void flock(ArrayList<Boid> boids) {
    PVector sep = separate(boids);   // Separation
    PVector ali = align(boids);      // Alignment
    PVector coh = cohesion(boids);   // Cohesion
    // Arbitrarily weight these forces
    sep.mult(1.5);
    ali.mult(1.0);
    coh.mult(1.0);
    // Add the force vectors to acceleration
    applyForce(sep);
    applyForce(ali);
    applyForce(coh);
  }

  // Method to update position
  void update() {
    // Update velocity
    velocity.add(acceleration);
    // Limit speed
    velocity.limit(maxspeed);
    position.add(velocity);
    // Reset accelertion to 0 each cycle
    acceleration.mult(0);
  }

  // A method that calculates and applies a steering force towards a target
  // STEER = DESIRED - VELOCITY
  PVector seek(PVector target) {
    PVector desired = PVector.sub(target, position);  // A vector pointing from the position to the target
    // Scale to maximum speed
    desired.normalize();
    desired.mult(maxspeed);

    // Steering = Desired minus Velocity
    PVector steer = PVector.sub(desired, velocity);
    steer.limit(maxforce);  // Limit to maximum steering force
    return steer;
  }

  void render() {
    // Draw a triangle rotated in the direction of velocity
    float theta = velocity.heading() + radians(90);
    
    fill(200, 100);
    stroke(255);
    pushMatrix();
    translate(position.x, position.y);
    rotate(theta);
    beginShape(TRIANGLES);
    vertex(0, -r*2);
    vertex(-r, r*2);
    vertex(r, r*2);
    endShape();
    popMatrix();
  }

  // Wraparound
  void borders() {
    if (position.x < -r) position.x = width+r;
    if (position.y < -r) position.y = height+r;
    if (position.x > width+r) position.x = -r;
    if (position.y > height+r) position.y = -r;
  }

  // Separation
  // Method checks for nearby boids and steers away
  PVector separate (ArrayList<Boid> boids) {
    float desiredseparation = 25.0f; // Minimum distance
    PVector steer = new PVector(0, 0);
    int count = 0;
    // For every boid in the system, check if it's too close
    for (Boid other : boids) {
      float d = PVector.dist(position, other.position);
      // If the distance is greater than 0 and less than an arbitrary amount (0 when you are yourself)
      if ((d > 0) && (d < desiredseparation)) {
        // Calculate vector pointing away from neighbor
        PVector diff = PVector.sub(position, other.position);
        diff.normalize();
        diff.div(d);        // Weight by distance
        steer.add(diff);
        count++;            // Keep track of how many
      }
    }
    // Average -- divide by how many
    if (count > 0) {
      steer.div((float)count);
    }

    // As long as the vector is greater than 0
    if (steer.mag() > 0) {
      // Implement Reynolds: Steering = Desired - Velocity
      steer.normalize();
      steer.mult(maxspeed);
      steer.sub(velocity);
      steer.limit(maxforce);
    }
    return steer;
  }

  // Alignment
  // For every nearby boid in the system, calculate the average velocity
  PVector align (ArrayList<Boid> boids) {
    float neighbordist = 50;  // neighbor distance
    PVector sum = new PVector(0, 0);
    int count = 0;
    for (Boid other : boids) {
      float d = PVector.dist(position, other.position);
      if ((d > 0) && (d < neighbordist)) {
        sum.add(other.velocity);
        count++;
      }
    }
    if (count > 0) {
      sum.div((float)count);
      // Implement Reynolds: Steering = Desired - Velocity
      sum.normalize();
      sum.mult(maxspeed);
      PVector steer = PVector.sub(sum, velocity);
      steer.limit(maxforce);
      return steer;
    } 
    else {
      return new PVector(0, 0);
    }
  }

  // Cohesion
  // For the average position (i.e. center) of all nearby boids, calculate steering vector towards that position
  PVector cohesion (ArrayList<Boid> boids) {
    float neighbordist = 50;  // neighbor distance
    PVector sum = new PVector(0, 0);   // Start with empty vector to accumulate all positions
    int count = 0;
    for (Boid other : boids) {
      float d = PVector.dist(position, other.position);
      if ((d > 0) && (d < neighbordist)) {
        sum.add(other.position); // Add position
        count++;
      }
    }
    if (count > 0) {
      sum.div(count);
      return seek(sum);  // Steer towards the position
    } 
    else {
      return new PVector(0, 0);
    }
  }
}

クラスを使わない簡略化したソース例

クラスの設計やPVectorを使用していない例である。簡潔に記述されている。

https://garchiving.com/algorithm-of-boids-with-processing/

  • 1羽の鳥の位置ベクトルは(x,y)、速度の単位ベクトルは(dx,dy) 
int num = 80;

float[] x  =new float[num];
float[] y  =new float[num];
float[] r  =new float[num];
float[] dx  =new float[num];
float[] dy  =new float[num];

float[] ctrDirX =new float[num];    
float[] ctrDirY =new float[num];    
float[] vel =new float[num];
float[] velAngle =new float[num];
float[] contX =new float[num];    
float[] contY =new float[num];    
float[] kX =new float[num];    
float[] kY =new float[num];    

float aveX, aveY, aveAngle, aveVel;
float velX, velY;

void setup() {
  for (int i=0; i<num; i++) {
    r[i]     = 10;
    x[i]     = 250+80*cos(radians((360/num)*i));
    y[i]     = 250+80*sin(radians((360/num)*i));
    velAngle[i] = (360/num)*i;
    vel[i]   = random(0, 5.5);
    dx[i]    = vel[i]*cos(radians(velAngle[i]));
    dy[i]    = vel[i]*sin(radians(velAngle[i]));
  }

  size(800, 800);
  background(240);
  smooth();
}

void draw() {
  background(240);
  stroke(100);
  strokeWeight(1);
  noFill();
  for (int i=0; i<num; i++) {
    ellipse(x[i], y[i], 10, 10);
    line(x[i], y[i], x[i]+10*dx[i], y[i]+10*dy[i]);
  }

// Cohesion
  aveX = 0;
  aveY = 0;
  for (int i=0; i<num; i++) {
    aveX += x[i];
    aveY += y[i];
  }
  aveX /= num;
  aveY /= num;
  if (mousePressed == true) {
    aveX = mouseX;
    aveY = mouseY;
    stroke(0, 0, 255);
    fill(0, 0, 255);
    ellipse(aveX, aveY, 10, 10);
  } 

  for (int i=0; i<num; i++) {
    ctrDirX[i] = aveX - x[i];
    ctrDirY[i] = aveY - y[i];
  }

// Align
  aveVel   = 0;
  aveAngle = 0;
  for (int i=0; i<num; i++) {
    aveVel   += sqrt(dx[i]*dx[i]+dy[i]*dy[i]);
    aveAngle += degrees(atan2(dy[i], dx[i]));
  }
  aveVel   /= num;
  aveAngle /= num;

  velX = aveVel*cos(radians(aveAngle));
  velY = aveVel*sin(radians(aveAngle));

// Separate
  for (int i=0; i<num; i++) {
    contX[i]=0;
    contY[i]=0;
    for (int j=0; j<num; j++) {
      if (i!=j) {
        float dist=sqrt((x[j]-x[i])*(x[j]-x[i])+(y[j]-y[i])*(y[j]-y[i]));
        if (0<dist&&dist<15) {
          contX[i] = -1*(x[j]-x[i]);
          contY[i] = -1*(y[j]-y[i]);
          float temp = sqrt(contX[i]*contX[i]+contY[i]*contY[i]);
          contX[i]/=temp;
          contY[i]/=temp;
        }
      }
    }
  }

// Cohesion + Allgin + Separate
  for (int i=0; i<num; i++) {
    kX[i] = 0.03*ctrDirX[i]+4.0*velX+5.0*contX[i];
    kY[i] = 0.03*ctrDirY[i]+4.0*velY+5.0*contY[i];

    float tempVel = sqrt(kX[i]*kX[i]+kY[i]*kY[i]);
    if (tempVel>2) {
      kX[i]=2*kX[i]/tempVel;
      kY[i]=2*kY[i]/tempVel;
    }

    dx[i] += (kX[i]-dx[i])*0.02;
    dy[i] += (kY[i]-dy[i])*0.02;

    x[i] += dx[i];
    y[i] += dy[i];
    
    if (x[i]>width)x[i]=0;
    if (x[i]<0)x[i]=width;
    if (y[i]>height)y[i]=0;
    if (y[i]<0)y[i]=height;
  }
}

人工生命(ALife)

セルオートマトン

ラングトンのアリ

反応拡散系

フラクタル

参考

スケーラブルアート論

「http://w3.kuhalabo.net/wiki/index.php?title=%E3%83%AC%E3%82%A4%E3%83%8E%E3%83%AB%E3%82%BA%E3%81%AE%E3%83%9C%E3%82%A4%E3%83%89&oldid=2826」から取得
個人用ツール
名前空間

変種
操作
案内
ツールボックス