自己相似形
提供:kuhalaboWiki
目次 |
再帰的呼出しによる樹木の描画
- 再帰的( recursive )呼び出しとは,サブルーチンや関数が,自分自身を呼び出すことをいう。樹木は,枝の1つを取り出して拡大しても,元の枝と同じ形(相似形)をしている。これは,同じサブルーチンで枝を描画しているからである。
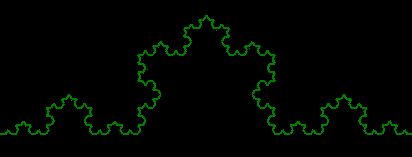
コッホ図形の描画
- Recursクラスの作成
- Recurs.h
#pragma once
#include "ofMain.h"
#include <math.h> //算術関数の読み込み
class Recurs {
public:
ofColor bcolor; //描画色
int generation; // 世代
void koch(int n, ofPoint p1, ofPoint p2); //再帰的呼び出しメソッド
};
- Recurs.cpp
#include "Recurs.h"
//三角関数の値をstaticグローバル定数として定義
static const double S60 = sin( PI / 3.0); // sin(60)
static const double C60 = cos( PI / 3.0); // cos(60)
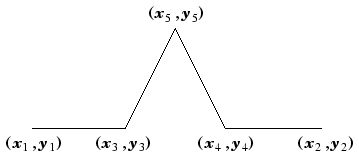
void Recurs::koch(int n, ofPoint p1, ofPoint p2){
ofPoint p3,p4,p5;
if( n > 0 ){
p3 = ( 2 * p1 + p2 ) / 3.0; //内分点
p4 = ( p1 + 2 * p2 ) / 3.0;
p5.x = p3.x + ( p4.x - p3.x ) * C60 + (p4.y - p3.y) * S60; //回転移動
p5.y = p3.y - ( p4.x - p3.x ) * S60 + (p4.y - p3.y) * C60;
ofSetColor(0,0,0);
ofLine(p3,p4); //余分な線を消す
ofSetColor(bcolor);
ofLine(p1,p3); //線分の描画
ofLine(p3,p5);
ofLine(p5,p4);
ofLine(p4,p2);
koch( n-1, p1, p3); //再帰呼び出し n>0
koch( n-1, p3, p5);
koch( n-1, p5, p4);
koch( n-1, p4, p2);
}
}
- ofApp.h
#pragma once
#include "ofMain.h"
#include "Recurs.h"
class ofApp : public ofBaseApp{
public:
void setup();
void update();
void draw();
void keyPressed(int key);
void keyReleased(int key);
void mouseMoved(int x, int y );
void mouseDragged(int x, int y, int button);
void mousePressed(int x, int y, int button);
void mouseReleased(int x, int y, int button);
void windowResized(int w, int h);
void dragEvent(ofDragInfo dragInfo);
void gotMessage(ofMessage msg);
Recurs myKoch;
ofPoint pos1;
ofPoint pos2;
};
- ofApp.cpp
#include "ofApp.h"
//--------------------------------------------------------------
void ofApp::setup(){
ofBackground(0, 0, 0); //背景色の設定
ofSetFrameRate(30); //フレームレイト設定
pos1 = ofPoint(ofGetWidth()*1/4, ofGetHeight()*2/4);//初期点の設定
pos2 = ofPoint(ofGetWidth()*3/4, ofGetHeight()*2/4);
myKoch.generation = 5; //世代の設定
myKoch.bcolor = ofColor(0,255,0); //描画色の設定
}
//--------------------------------------------------------------
void ofApp::update(){
}
//--------------------------------------------------------------
void ofApp::draw(){
myKoch.koch(myKoch.generation, pos1, pos2);
}
動かしてみる
- Recursクラスに現在位置と速度のプロパティを追加
- Recurs.h
class Recurs {
public:
ofColor bcolor; //描画色
int generation; // 世代
ofPoint pos1;
ofPoint pos2;
ofPoint vel1;
ofPoint vel2;
Recurs();
void koch(int n, ofPoint p1, ofPoint p2); //再帰的呼び出しメソッド
- ofApp.cpp
- setupe()で初期の位置、速度、世代数、描画色を設定
- update()で位置と速度を更新
//--------------------------------------------------------------
void ofApp::setup(){
ofBackground(0, 0, 0); //背景色の設定
ofSetFrameRate(30); //フレームレイト設定
myKoch.pos1 = ofPoint(ofGetWidth()*1/4, ofGetHeight()*2/4);
myKoch.vel1 = ofPoint(ofRandom(-5,5),ofRandom(-3,3));
myKoch.pos2 = ofPoint(ofGetWidth()*3/4, ofGetHeight()*2/4);
myKoch.vel2 = ofPoint(ofRandom(-5,5),ofRandom(-3,3));
myKoch.generation = 7; //世代の設定
myKoch.bcolor = ofColor(0,255,0); //描画色の設定
}
//--------------------------------------------------------------
void ofApp::update(){
myKoch.pos1 += myKoch.vel1;
myKoch.pos2 += myKoch.vel2;
if(myKoch.pos1.x > ofGetWidth() || myKoch.pos1.x < 0){
myKoch.vel1.x *= -1;
}
if(myKoch.pos1.y > ofGetHeight() || myKoch.pos1.y < 0){
myKoch.vel1.y *= -1;
}
if(myKoch.pos2.x > ofGetWidth() || myKoch.pos2.x < 0){
myKoch.vel2.x *= -1;
}
if(myKoch.pos2.y > ofGetHeight() || myKoch.pos2.y < 0){
myKoch.vel2.y *= -1;
}
}
//--------------------------------------------------------------
void ofApp::draw(){
myKoch.koch(myKoch.generation, myKoch.pos1, myKoch.pos2);
}
ドラゴン図形の描画
- dragon()メソッドの追加
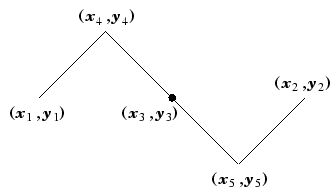
void Recurs::dragon(int n, ofPoint p1, ofPoint p2){
ofPoint p3,p4,p5;
if( n > 0 ){
p3 = ( p1 + p2 ) / 2.0; //内分点
p4.x = ( p1.x + p3.x - p1.y + p3.y ) / 2.0;
p4.y = ( p1.x - p3.x + p1.y + p3.y ) / 2.0;
p5.x = ( p2.x + p3.x - p2.y + p3.y ) / 2.0;
p5.y = ( p2.x - p3.x + p2.y + p3.y ) / 2.0;
ofSetColor(0,0,0);
ofLine(p1,p3); //余分な線を消す
ofLine(p3,p2); //余分な線を消す
ofSetColor(bcolor);
ofLine(p1,p4); //線分の描画
ofLine(p4,p3);
ofLine(p3,p5);
ofLine(p5,p2);
dragon( n-1, p1, p4); //再帰呼び出し n>0
dragon( n-1, p4, p3); //再帰呼び出し n>0
dragon( n-1, p3, p5); //再帰呼び出し n>0
dragon( n-1, p5, p2); //再帰呼び出し n>0
}
}
シダ葉の描画
- ドラゴン図形の変化形
- ドラゴン図形で使用した(x1,y1), (x2,y2), (x3,y3), (x4,y4), (x5,y5)を使う
- 直線(x1,y1)-(x2,y2), 直線(x1,y1)-(x4,y4), 直線(x3,y3)-(x5,y5)を基本図形とする。
- sida()メソッドの追加
Cカーブの描画
- ccurve()メソッドの追加
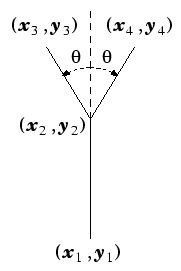
樹木の描画
- Taneクラスのメソッド
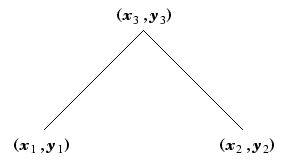
線分(x1,y1)-(x2,y2)が与えられたら、(x2,y2)の先端に(x3,y3), (x4,y4)を取り、線分(x2,y2)-(x3,y3)と線分(x2,y2)-(x4,y4)を描画する。
- jumoku()メソッドの追加