フラクタル
提供:kuhalaboWiki
(版間での差分)
(→KochLineクラス) |
(→KochFractalクラス) |
||
| 196行: | 196行: | ||
return end.get(); | return end.get(); | ||
} | } | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
</pre> | </pre> | ||
2020年11月2日 (月) 08:33時点における版
目次 |
概要
古代ギリシャからあるユークリッド幾何学と20世紀のフラクタル幾何学の比較
- 考察
- 古代エジプト人は3:4:5の辺を持つ三角形で直角が得られることを知っていた.ピラミッドなどの巨大建造物.
- 三平方の定理を発見したピタゴラスはどこがすごいか?
- Nature of Code, Ch 8 Fractals
- https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals
再帰的呼び出し
再帰的(recursive)呼び出しとは,サブルーチンや関数が,自分自身を呼び出すアルゴリズムをいう。 これを利用すると,複雑な手順を簡潔に記述することができる。
- 再帰的(Recursive)呼び出し
- "Recursive"という言葉を「頭山的」と訳した人がいる。
- 落語「自分の頭の上に穴があいて池ができた。その人が将来を悲観して,その池に身を投げた」
- 再帰的な定義の例: GNU: " GNU is Not Unix "
再帰は数学的帰納法であり,「局所的なルールで全体を記述する」ことである。 i)最初のコマを倒す。ii)n番目のコマが倒れると,n+1番目のコマも倒れる。iii)すべてのコマが倒れる。
- nの階乗を再帰と反復で計算する際の比較
- n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1
- 1! = 1
// 再帰:n!=n*(n-1)! という漸化式で計算する。
int factorial(int n){
if (n == 1){
return 1;
}else{
return n * factorial(n-1); //再帰的呼び出し
}
}
// 反復:1からnまでを乗算する。
int factorial(int n){
int f = 1;
for (int i = 0; i < n; i++){
f = f * (i+1);
}
return f;
}
再帰的な円
void setup() {
size(640,360);
}
void draw() {
background(255);
drawCircle(width/2,height/2,400);
noLoop();
}
// Recursive function
void drawCircle(float x, float y, float r) {
stroke(0);
noFill();
ellipse(x, y, r, r);
if(r > 2) {
// Now we draw two more circles, one to the left
// and one to the right
drawCircle(x + r/2, y, r/2);
drawCircle(x - r/2, y, r/2);
}
}
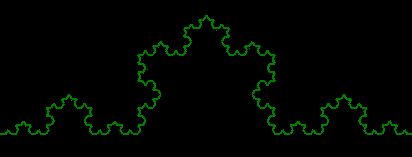
コッホ図形
全体
// Koch Curve
// Renders a simple fractal, the Koch snowflake
// Each recursive level drawn in sequence
ArrayList<KochLine> lines ; // A list to keep track of all the lines
void setup() {
size(383, 200);
background(255);
lines = new ArrayList<KochLine>();
PVector start = new PVector(0, 150);
PVector end = new PVector(width, 150);
lines.add(new KochLine(start, end));
for (int i = 0; i < 5; i++) {
generate();
}
smooth();
}
void draw() {
background(255);
for (KochLine l : lines) {
l.display();
}
}
void generate() {
ArrayList next = new ArrayList<KochLine>(); // Create emtpy list
for (KochLine l : lines) {
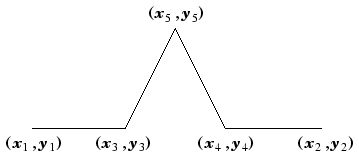
// Calculate 5 koch PVectors (done for us by the line object)
PVector a = l.kochA();
PVector b = l.kochB();
PVector c = l.kochC();
PVector d = l.kochD();
PVector e = l.kochE();
// Make line segments between all the PVectors and add them
next.add(new KochLine(a, b));
next.add(new KochLine(b, c));
next.add(new KochLine(c, d));
next.add(new KochLine(d, e));
}
lines = next;
}
KochLineクラス
// Koch Curve
// A class to describe one line segment in the fractal
// Includes methods to calculate midPVectors along the line according to the Koch algorithm
class KochLine {
// Two PVectors,
// a is the "left" PVector and
// b is the "right PVector
PVector start;
PVector end;
KochLine(PVector a, PVector b) {
start = a.get();
end = b.get();
}
void display() {
stroke(0);
line(start.x, start.y, end.x, end.y);
}
PVector kochA() {
return start.get();
}
// This is easy, just 1/3 of the way
PVector kochB() {
PVector v = PVector.sub(end, start);
v.div(3);
v.add(start);
return v;
}
// More complicated, have to use a little trig to figure out where this PVector is!
PVector kochC() {
PVector a = start.get(); // Start at the beginning
PVector v = PVector.sub(end, start);
v.div(3);
a.add(v); // Move to point B
v.rotate(-radians(60)); // Rotate 60 degrees
a.add(v); // Move to point C
return a;
}
// Easy, just 2/3 of the way
PVector kochD() {
PVector v = PVector.sub(end, start);
v.mult(2/3.0);
v.add(start);
return v;
}
PVector kochE() {
return end.get();
}
}