スケーラブルアート論
(→Processing公式サイトのソース例) |
(→Processing公式サイトのソース例) |
||
| 2,042行: | 2,042行: | ||
* pushMatrix(), translate(x,y);rotate(theta);beginShape();vertex();endShape();popMatrix();を使った鳥(三角形)の描画 | * pushMatrix(), translate(x,y);rotate(theta);beginShape();vertex();endShape();popMatrix();を使った鳥(三角形)の描画 | ||
| − | * | + | */ [https://qiita.com/hp0me/items/7d6483e0a34297005938 操舵行動・追跡] / [http://www.red3d.com/cwr/steer/ Steering] |
| − | + | ** [https://gamedevelopment.tutsplus.com/tutorials/understanding-steering-behaviors-seek--gamedev-849 seek(追跡)] / [https://gamedevelopment.tutsplus.com/tutorials/understanding-steering-behaviors-flee-and-arrival--gamedev-1303 flee(逃避)] | |
| − | + | ||
*クラスの設計 | *クラスの設計 | ||
2020年10月28日 (水) 00:39時点における版
目次 |
概要
- 前提スキル
一年生の時にメディアプログラミング演習Iを履修したのと同等のプログラミングスキルがあるものとして、授業を進めます。 もし、プログラミングに不安があるなら、上記テキストを使って、自分で予習や自習をしてください。 openFrameworksはProcessingと似ているため、Processingを知っていると、理解が早いです。
- 成績評価
確認テスト、課題で評価します。
- 授業概要及び到達目標
- インタラクティブアートは芸術を基盤として科学や工学を統合する新しい領域である。生物科学に関連した分野として、人工生命、ライフゲーム、フラクタル、オートマトン、遺伝的アルゴリズム、ニューラルネットワークなど応用範囲の広いものが数多く存在する。
そういった生物に見られる特徴をアートに応用したジェネラティブアートの作品をC++のプログラミングを使用して、実際に作成してみる。
本講義の目標は以下の通り。
- 生物の特徴と生物的なシステムについて理解する。
- 複雑系システムについて理解し、応用例を作成できる。
- openFrameworksを使って作品のプログラミングができる。
開発環境
開発環境としてopenFrameworks/MacOS XCode, Processing, p5.jsを使用します。
テキストや開発環境については、以下を参照してください。
- openframeworks https://openframeworks.cc/ja/
- http://www.kuhalabo.net/kxoops/modules/d3blog/details.php?bid=141
- https://processing.org/
- p5.js http://p5js.org
- ドットインストールp5.js入門 http://dotinstall.com/lessons/basic_p5js
- Generative Design with p5.js http://www.generative-gestaltung.de/
- Generative Art with Math https://www.openprocessing.org/user/57914
予定
- 2020年度
- 9/25(金) ガイダンス,
- Processingの準備
- 生物と情報とアート
- 10/2(金) 最大公約数と矩形分割
- ユークリッドの互除法(最大公約数)
- 長方形を正方形で分割
- 正方形の分割
- 矩形の再帰的分割
- 10/9(金) 矩形分割とフィボナッチ数列
- 無理数比の矩形分割
- モンドリアンのCompositionの再現
- フィボナッチ数列の可視化
- フィボナッチらせん
- 再帰的描画のらせん
- 10/16(金) フィボナッチ数列とらせん
- フェルマーらせん
- 離散的らせん
- 10/23(金) プログラミング課題制作1、遺伝的アルゴリズム(講義)
- 10/30(金)1次元セルオートマトン
- パスカルの3角形
- 基本セルオートマトン
- 11/6(金) 2次元セルオートマトン
- 正方格子
- ライフゲーム
- 正6角形ライフゲーム
- 11/13(金) ラングトンのアリ
- 11/20(金) Boid https://processing.org/examples/flocking.html
- 11/27(金)反応拡散系モデル
- 12/4(金) フラクタル http://ariga.dwcmedia.jp/ProcessingWeb/Trail8Fractal.html
- 12/11(金) プログラミング課題制作2 、ニューラルネットワーク(講義)
- 12/18(金) まとめ確認テスト
- 2019年度
- 9/13(金) ガイダンス, 生物と情報とアート,openFrameworksプログラミング体験
- 9/20(金) 生物と情報とアート,XCodeを使用したopenFrameworksプログラミング実習
- 9/27(金) 幾何学図形の描画
- (oF実習)
- 教科書 1章 読み物として読む。
- 教科書 2章 実際にプログラムを作ってみる。
- 2-4「数値の記憶と計算」までをやり終えて、自作プログラムの実行ファイルを提出。
- 幾何学図形の描画、色の設定、変数
- プロジェクトフォルダーのbinフォルダーの中にあります。
- ファイル名 番号_名前のローマ字 例 1724000_suzukiichiro
- 講義: ディープラーニングによる色の芸術的表現1
- 完全情報確定ゼロサムゲーム、アルゴリズムとヒューリスティック、エキスパートシステム
- (oF実習)
- 10/4(金) 幾何学図形の描画
- (oF実習)
- 2-8「条件分岐」までを学習し、自作プログラム実行ファイルを提出。
- 繰り返し、配列、図形の移動、条件分岐
- 講義: ディープラーニングによる色の芸術的表現2
- ディープラーニング
- (oF実習)
- 10/11(金)
- (oF実習)
- 2-11「より高度な表現」までを学習し、自作プログラムの実行ファイルを提出。
- マウスアクション、摩擦、重力、軌跡のフェード
- この日の授業までに2章を終えてください。2章までに学んで、制作したプログラムを提出してもらいます。
- 講義:最大公約数と矩形分割
- 10/18(金)
- (P5実習)
- Generative Art with MathのCh1, Ch2を学ぶ。
- (oF実習)
- 3-1,2,3を学習する。
- 3-1 は、読んで理解してください。プログラム例は作らなくてもよいです。
- 3-2 は、3-2-7「画像ファイルを扱う」だけでもよい。余裕がれば、他の単元を勉強してもよいです。、
- 3-3 は、実際に新たにクラスを作成し、プログラムを作りながら、学習を進めてください。
- 3-4「アドオンの利用」以降は学習しなくてもよい。関心に応じて学習してください。
- 講義:らせん
- 10/25(金)
- 11/8(金)
- (実習)離散的らせん
- 講義:1次元セルオートマトン
- 11/15(金)
- (実習)1次元セルオートマトン
- 講義:2次元セルオートマトン、ライフゲーム
- 11/22(金)
- (実習)2次元セルオートマトン、ライフゲーム
- 講義:ラングトンのアリ
- 11/29(金)
- (実習)ラングトンのアリ
- 講義:Boid,Gray-Scott反応拡散系モデル
- 12/6(金)
- (実習)
- 講義:物理エンジン Box2D,フラクタルと自己相似形と再帰呼び出し
- 12/13(金)
- (実習)Box2D,自己相似形と再帰呼び出し
- 講義:ニューラルネットワーク、遺伝的アルゴリズム
- 12/20(金) 小テスト ,課題講評
- 授業で扱った内容すべてが含まれます。
- 1/10(金) 予備日(出席は取りません)
- 課題「創発ジェネラティブアートのプログラム」
- 提出締切日 12/19(木)
- 授業で扱ったプログラムを土台として、自分のオリジナリティを加えた創発的なプログラムを提出してください。
- 言語は、ProcessingかopenFrameworksのいずれかです。
- ソースプログラムも採点の対象としますので、プロジェクトのフォルダー全体をzip圧縮して、提出して下さい。
- Contents
- Scalable art, Generative art, Mathematical art, Artificial Intelligence, Artificial Life, Complext sysytem
- openFrameworks C++ / Xcode MacOSX
- Logic circuit
- 完全情報ゲーム:チェッカー、オセロ、チェス、将棋、囲碁
- Cell auttomaton
- Conway's game of life
- Wire world
- Random walk
- Langton's ant
- Boid
- Box2D
- Fractal, Self-similar
- Recursive call
- Complex square
- Mandelbrot
- Neural network
- Genetic algorithm
- Code, Chyper, Encript
- Space X
- Robotics
- Expert system
- Fourier transform, spectrum
- Fibonacci number
- Belousov-Zhabotinsky reaction
- Gray-Scott model
- Turing pattern
資料
- oF 0.9.x 1からの変更点 https://qiita.com/2bbb/items/13f2e20760ec61e3ec89
- new ⇐ old
- ofDrawLine ⇐ ofLine
- ofDrawCurve ⇐ ofCurve
- ofDrawBezier ⇐ ofBezier
- ofDrawCircle ⇐ ofCircle
- ofDrawEllipse ⇐ ofEllipse
- ofDrawTriangle ⇐ ofTriangle
- ofDrawRectangle ⇐ ofRect
- ofDrawRectRounded ⇐ ofRectRounded
- ofDrawSphere ⇐ ofSphere
- ofDrawCone ⇐ ofCone
- ofBox ⇐ ofDrawBox
oF新規プロジェクトの作成
- oFフォルイダー内のprojectGeneratorフォルダー内のprojectGeneratorを実行する。
- Project Path:にoFのあるフォルダーを指定する。
- Project Name:に、プロジェクトの名前を入れる。
- Addons:に、使用する追加機能(アドオン)を入れる。通常は、なしでよい。
- Generateをクリックする。
- Apps内のMyAppsにマイプロジェクトが作成されている。
- Open IDEをクリックした場合
- XCodeが立ち上がることを確認する。
- Closeをクリックした場合
- Apps内のMyAppsに作成したプロジェクトフォルダーを開く。
- プロジェクト名.xcodeprojファイルをクリックして、XCodeを起動する。
- 作成したプロジェクトを起動し、srcを見てみる。
- ofApp.cppのメソッドの中身が空っぽ。
- ここにプログラムを書いていく。
oFクラスの作成
XCode
- 新しくクラスを作るには、「Fileメニュー > New > File」 を開く。
- 「macOS」タブの「Source」から、「C++ File」を選び、「Next」ボタンを押す。
- Nameにはクラス名を入れます。その際、「Also create a header file」のチェックを入れておきます。そして「Next」ボタンを押します。
- 名前を それぞれXxx.cpp,Xxx.hとし、場所はともに ..\src とする。
- srcの中にXxx.cpp と Xxx.h が新規作成される。
Visual Studio
- 新しくクラスを作るには、「プロジェクト > 新しい項目の追加...」 を開き,「C++ファイル」と「ヘッダーファイル」を一つずつ作る。
- 名前を それぞれXxx.cpp,Xxx.hとし、場所はともに ..\src とする
- (注)「クラスの追加」や「クラスウィザード」は使えない。
- マウスカーソルをソリューションエクスプローラー上のsrcに置き、ハイライトさせる。
- ソリューションエクスプローラー上のsrcの中にXxx.cpp と Xxx.h が新規作成される。
ヘッダファイル Xxx.h は,
#pragma once
#include "ofMain.h"
class Xxx {
private:
ofPoint pos;
float radius;
public:
Xxx();
void hogehoge();
};
などと、記述する。
- ofMain.h をインクルードし、クラスの定義の最後にセミコロンがつくことに注意する。
- #pragma once は,このヘッダファイルを複数回読み込まないようにするためのもの。
- 括弧で囲まれた部分 {...} には,変数の宣言やメソッド(関数)の宣言を書く
- private: に続く部分には,クラス内部のみで利用する変数、メソッドを宣言する。
- public: に続く部分には,クラス外部からアクセスできる変数、メソッドを宣言する。
- Xxx(): はコンストラクターといい、クラスと同じ名前のメソッドである。クラスのインスタンスを生成するときの初期化処理などを記述する。
C++ファイル Xxx.cpp は,
#include "Xxx.h" // クラスのヘッダーを読み込む
Xxx::Xxx(){
pos = ofPoint(ofGetWidth()/2, ofGetHeight()/2);
radius = 100.0;
}
void Xxx::hogehoge(){
ofSetColor(31, 63, 255, 100);
ofCircle(pos.x, pos.y, radius);
ofSetColor(255, 0, 0, 200);
ofCircle(pos.x, pos.y, radius);
}
などと、メソッドの本体を記述する。
- メソッドの定義の最後にセミコロンがつかないことに注意する。
もとのcppファイルodApp.cppのヘッダーファイルofApp.hに、Xxx.hをincludeする。
例えば、ofApp.hは、以下のとおり。
#pragma once
#include "ofMain.h"
#include "Ball.h"
class ofApp : public ofBaseApp{
public:
bool mouse_pressed;
public:
void setup();
void update();
void draw();
void keyPressed(int key);
void keyReleased(int key);
void mouseMoved(int x, int y );
void mouseDragged(int x, int y, int button);
void mousePressed(int x, int y, int button);
void mouseReleased(int x, int y, int button);
void windowResized(int w, int h);
void dragEvent(ofDragInfo dragInfo);
void gotMessage(ofMessage msg);
Xxx myCbj;
};
publicの領域にXxxクラスのインスタンスmyObjを宣言している。
生物と情報とアート
- 生物とは? 生物の特徴とは?
- 例:小石と貝殻
- 「生物と無生物の違いは何か?」説明してみよう。
- ゲノムのDNAマップ NCBI Genome Map Viewer
- ヒト一人を再生するのに必要な情報量は?
- 自己相似性、フラクタル
- 雪の結晶(0:25)
- 樹木(1:17)
- オウム貝(1:30)
- らせん、渦巻き状パターン
- 黄金角とフィボナッチ数列(3:00)
論理回路
https://wwws.kobe-c.ac.jp/deguchi/sc180/logic/gate.html
最大公約数と矩形分割
- 現代アート作家 モンドリアンの代表作品、Composition
- https://www.youtube.com/watch?v=dJmY4QhplBE (モンドリアンの作品全般の紹介、Compositionは6:01あたりから)
- https://www.youtube.com/watch?v=q21SA9NHSds(モンドリアンのComposition)
- https://www.youtube.com/watch?v=FqoZiUetwLs&t=1s (Compositionを題材にした動画)
最大公約数
- 例
- 4と6の最大公約数は2
- 12と18の最大公約数は6
- 24と36の最大公約数は12
- 123と456の最大公約数は…3
- 912と1368の最大公約数は???…456
- ユークリッドの互除法
- https://ja.wikipedia.org/wiki/%E3%83%A6%E3%83%BC%E3%82%AF%E3%83%AA%E3%83%83%E3%83%89%E3%81%AE%E4%BA%92%E9%99%A4%E6%B3%95
- https://www.sist.ac.jp/~kanakubo/research/hosoku/euclid_gojo.html
- 自然数x0,x1の最大公約数の求め方(x0 > x1)
- x0をx1で割り、余りをx2とする。
- x1をx2で割り、余りをx3とする。
- 割り切れるまで、この操作を繰り返す。
- xNで割り切れたら、xNが最大公約数である。
//aとbに対してユークリッド互除法を行う
int a = 10;
int b = 6;
int c; //商のための変数
int d = b; //余りのための変数
int itr = 0; //繰り返しの回数
//繰り返し処理
while (d > 0){ //余りが0以上のとき以下の処理を実行
itr++; //繰り返し回数を1増やす
c = a / b; //cに商を代入
d = a % b ; //dに余りを代入
println(itr, ":", a, "/", b, "=", c, "...", d); //計算結果を表示
a = b; //aにbを代入
b = d; //bに余りを代入
}
println("GCD is", a); //最大公約数を表示
長方形の分割
- ユークリッドの互除法を可視化してみる。
- 自然数x0,x1を2辺とする長方形を正方形で分割する。
- 最も小さい正方形の1辺が最大公約数
- 復習:点、線、図形の描画
- DivRect
//横縦比がnumA:numBの長方形を正方形によって分割
int numA = 10;
int numB = 6;
int scalar = 50; //長方形の拡大倍率
numA *= scalar; //数値の大きさを拡大
numB *= scalar;
//プログラム実行中に動く変数
int wd = numB; //分割に使う正方形の幅の大きさ(初期値numB)
int xPos = 0; //正方形のx位置(初期値0)
int yPos = 0; //正方形のy位置(初期値0)
int itr = 0; //分割の繰り返し回数(初期値0)
//描画
size(500, 500); //描画ウィンドウサイズ
//繰り返し処理
while (wd > 0){ //幅が0になるまで以下を実行
itr++; //繰り返し回数を1増やす
if (itr % 2 == 1){ //繰り返し回数が奇数のとき,x軸方向へ正方形を増やす
while (xPos + wd <= numA){ //幅を足したとき,長方形を超えなければ以下を実行
rect(xPos, yPos, wd, wd); //(xPos,yPos)を左上の頂点とする1辺wdの正方形を描画
xPos += wd; //x位置を更新
}
wd = numA - xPos; //幅を更新
} else { //繰り返し回数が偶数のとき,y軸方向へ正方形を加える
while (yPos + wd <= numB){ //幅を足したとき,長方形を超えなければ以下を実行
rect(xPos, yPos, wd, wd); //(xPos,yPos)を左上の頂点とする1辺wdの正方形を描画
yPos += wd; //y位置を更新
}
wd = numB - yPos; //幅を更新
}
}
- 正方形に色を付けてみる
int numA = 10;
int numB = 6;
int scalar = 50;
numA *= scalar;
numB *= scalar;
int wd = numB;
int xPos = 0;
int yPos = 0;
int itr = 0;
//描画
size(500, 500);
color col; //色のための変数
colorMode(HSB, 1); //01区間をパラメータとするHSB色形式を使用
//ループ
while (wd > 0) {
itr++;
if (itr % 2 ==1) {
while (xPos + wd <= numA) {
col = color(random(1), 1, 1); //色相のみを01区間でランダムに変える
fill(col);
rect(xPos, yPos, wd, wd);
xPos += wd;
}
wd = numA - xPos;
} else {
while (yPos + wd <= numB) {
col = color(random(1), 1, 1);
fill(col);
rect(xPos, yPos, wd, wd);
yPos += wd;
}
wd = numB - yPos;
}
}
正方形の分割
自然数x0とx1の縦横比x0:x1を使って、長方形を正方形に変形すると、正方形を長方形に分割することになる。
- x0×x1の横長の長方形を x1/x0 に横方向に圧縮して正方形にする。
- DivSquare
//縦横比がnumA:numBの長方形によって正方形の描画ウィンドウを分割
int numA = 10;
int numB = 6;
float ratio = (float) numB / numA; //比率
float xPos = 0;
float yPos = 0;
int itr = 0;
//描画
size(500, 500);
colorMode(HSB, 1);
float wd = width; //描画ウィンドウの横幅サイズを初期値とする
//繰り返し処理
while (wd > 0.1){ //幅が許容誤差より大きければ以下を実行
itr++;
if (itr % 2 == 1){ //縦幅がwdの長方形をx軸方向へ加える
while (xPos + wd * ratio < width + 0.1){
//幅を足したとき,横幅がウィンドウを超えなければ以下の処理を実行
fill(color(random(1), 1, 1));
rect(xPos, yPos, wd * ratio, wd); //縦幅wd,縦横比がnumA:numBの長方形を描画
xPos += wd * ratio; //x位置を更新
}
wd = width - xPos;
} else { //横幅がwdの長方形をy軸方向へ加える
while (yPos + wd / ratio < width + 0.1){
//幅を足したとき,縦幅がウィンドウを超えなければ以下の処理を実行
fill(color(random(1), 1, 1)); //ランダムに色を指定
rect(xPos, yPos, wd, wd / ratio); //横幅wd,縦横比がnumA:numBの長方形を描画
yPos += wd / ratio; //y位置を更新
}
wd = width - yPos;
}
}
矩形の再帰的分割
長方形を正方形に分割し、その正方形を長方形に分割する。
//縦横比がnumB:numAの長方形を逆の比の長方形によって分割
int numA = 10;
int numB = 6;
float ratio = (float) numB / numA;
void setup(){ //最初に1度だけ実行する関数
size(500, 500);
colorMode(HSB, 1);
//この関数内だけのローカル変数
int itr = 0;
float xPos = 0;
float yPos = 0;
float wd = width * ratio;
while (wd > 0.1){
itr++;
if (itr % 2 == 1){
while (xPos + wd < width + 0.1){
divSquare(xPos, yPos, wd); //正方形を分割する関数の呼び出し
xPos += wd;
}
wd = width - xPos;
} else {
while (yPos + wd < width * ratio + 0.1){
divSquare(xPos, yPos, wd); //正方形を分割する関数の呼び出し
yPos += wd;
}
wd = width * ratio - yPos;
}
}
}
正方形を長方形に分割する関数
//位置(xPos,yPos)にある1辺がwdの正方形を縦横比がnumA:numBの長方形で分割する
void divSquare(float xPos, float yPos, float wd){
//この関数内だけのローカル変数
int itr = 0;
float xEndPos = wd + xPos; //正方形の右下の頂点のx座標
float yEndPos = wd + yPos; //正方形の右下の頂点のy座標
//繰り返し処理
while (wd > 0.1){
itr++;
if (itr % 2 == 1){
while (xPos + wd * ratio < xEndPos + 0.1){ //ratioはグローバル変数
fill(color(random(1), 1, 1));
rect(xPos, yPos, wd * ratio, wd);
xPos += wd * ratio;
}
wd = xEndPos - xPos;
} else {
while (yPos + wd / ratio < yEndPos + 0.1){
fill(color(random(1), 1, 1));
rect(xPos, yPos, wd, wd / ratio);
yPos += wd / ratio;
}
wd = yEndPos - yPos;
}
}
}
再帰的呼び出しの使用
- 正方形を長方形に分割し、その長方形を正方形に分割し、その正方形を長方形に分割し、・・・
- 再帰的に関数を呼び出す。再帰的呼び出し(Recursive Call)
- 再帰呼び出しを止めるしきい値(Threshold)を設定する。
int numA = 10;
int numB = 6;
float ratio = (float) numB / numA;
float thr = 160; //しきい値
void setup(){
size(500, 500);
colorMode(HSB, 1);
divSquare(0, 0, width); //正方形の分割
}
divSquare
//位置(xPos,yPos)にある1辺がwdの正方形を縦横比がnumA:numBの長方形で分割する
void divSquare(float xPos, float yPos, float wd){
int itr = 0;
float xEndPos = wd + xPos;
float yEndPos = wd + yPos;
fill(color(random(1), 1, 1));
rect(xPos, yPos, wd, wd);
while (wd > thr){ //wdがしきい値以上の場合に処理を行う
itr++;
if (itr % 2 == 1){
while (xPos + wd * ratio < xEndPos + 0.1){
divRect(xPos, yPos, wd * ratio); //長方形を分割する関数の呼び出し
xPos += wd * ratio;
}
wd = xEndPos - xPos;
} else {
while (yPos + wd / ratio < yEndPos + 0.1){
divRect(xPos, yPos, wd); //長方形を分割する関数の呼び出し
yPos += wd / ratio;
}
wd = yEndPos - yPos;
}
}
}
divRect
//位置(xPos,yPos)にある横幅wdで縦横比がnumA:numBの長方形を正方形によって分割する
void divRect(float xPos, float yPos, float wd){
int itr = 0;
float xEndPos = xPos + wd;
float yEndPos = yPos + wd / ratio;
fill(color(random(1), 1, 1));
rect(xPos, yPos, wd, wd / ratio);
while (wd > thr){ //長方形の幅がしきい値以上の場合に処理を行う
itr++;
if (itr % 2 == 0){
while (xPos + wd < xEndPos + 0.1){
divSquare(xPos, yPos, wd); //正方形を分割する関数の呼び出し
xPos += wd;
}
wd = xEndPos - xPos;
} else {
while (yPos + wd < yEndPos + 0.1){
divSquare(xPos, yPos, wd); //正方形を分割する関数の呼び出し
yPos += wd;
}
wd = yEndPos - yPos;
}
}
}
マウスクリックでx0,x1,thresholdをランダムに設定して描画する。
void mouseClicked(){
numA = int(random(1, 20)); //1以上20以下のランダムな整数を代入
numB = int(random(1, 20));
while (numA == numB){ //numAとnumBが異なるようにする
numB = int(random(1, 20));
}
thr = int(random(10,300));
println("numA =", numA, "numB =", numB,"thr =", thr); //numA,numB,thrの値を表示
ratio = (float) numA / numB;
background(0, 0, 1); //背景を白で消去
divSquare(0, 0, width);
}
void draw(){} //プログラムを実行している間,繰り返し実行する関数
無理数比の矩形分割
- モンドリアンの再現
//float ratio = sqrt(2); //白銀比
float ratio = (sqrt(5) + 1) / 2; //黄金比
//float ratio = (3 + sqrt(13) ) / 2; //青銅比
float thr = 40; //分割する大きさに関するしきい値
float thr2 = 0.5; //確率を決定するしきい値
void setup(){
size(500, 500);
colorMode(HSB, 1);
colorRect(0, 0, width, width);
divSquare(0, 0, width);
}
モンドリアン風に配色を決める
void colorRect(float xPos, float yPos, float wd, float ht){
color col;
float val = random(1);
if (val < 0.15){ //15%の確率
col = color(0, 1, 1); //赤
}else if (val < 0.3){ //15%の確率
col = color(2.0 / 3, 1, 1); //青
}else if (val < 0.45){ //15%の確率
col = color(1.0 / 6, 1, 1); //黄
}else if (val < 0.5){ //5%の確率
col = color(0, 1, 0); //黒
} else if (val < 0.7){ //20%の確率
col = color(0, 0, 0.9); //灰
} else { //30%の確率
col = color(0, 0, 1); //白
}
fill(col);
strokeWeight(5); //長方形の枠線の太さ
rect(xPos, yPos, wd, ht);
}
矩形分割
void divRect(float xPos, float yPos, float wd){ //長方形を分割する関数
int itr = 0;
float xEndPos = xPos + wd; //長方形の横の長さ
float yEndPos = yPos + wd / ratio; //長方形の縦の長さ
while (wd > thr){ //wdがしきい値以上の場合に処理を行う
itr++;
if (itr % 2 == 0){
while (xPos + wd < xEndPos + 0.1){
colorRect(xPos, yPos, wd, wd); //正方形を描く
if (random(1) < thr2){
divSquare(xPos, yPos, wd); //正方形を分割する関数の呼び出し
}
xPos += wd;
}
wd = xEndPos - xPos;
} else {
while (yPos + wd < yEndPos + 0.1){
colorRect(xPos, yPos, wd, wd); //正方形を描く
if (random(1) < thr2){
divSquare(xPos, yPos, wd); //正方形を分割する関数の呼び出し
}
yPos += wd;
}
wd = yEndPos - yPos;
}
}
}
void divSquare(float xPos, float yPos, float wd){ //正方形を分割する関数
int itr = 0;
float xEndPos = wd + xPos; //正方形の横の長さ
float yEndPos = wd + yPos; //正方形の縦の長さ
while (wd > thr){ //正方形の幅がしきい値以上の場合に実行
itr++;
if (itr % 2 ==1){
while (xPos + wd * ratio < xEndPos + 0.1){
colorRect(xPos, yPos, wd * ratio, wd); //長方形を描く
if (random(1) < thr2){ //thr2の確率で再分割
divRect(xPos, yPos, wd * ratio); //長方形を分割する関数の呼び出し
}
xPos += wd * ratio;
}
wd = xEndPos - xPos;
} else {
while (yPos + wd / ratio < yEndPos + 0.1){
colorRect(xPos, yPos, wd, wd / ratio); //長方形を描く
if (random(1) < thr2){ //thr2の確率で再分割
divRect(xPos, yPos, wd); //長方形を分割する関数の呼び出し
}
yPos += wd / ratio;
}
wd = yEndPos - yPos;
}
}
}
マウスクリックでランダムに再構成
void mouseClicked(){
thr = int(random(10, 50));
thr2 = random(0,1);
println("thr =", thr, "thr2 =", thr2);
colorRect(0, 0, width, width);
divSquare(0, 0, width);
}
void draw(){}
フィボナッチ数列
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81%E6%95%B0
- f(0) = 0, f(1) = 1, f(n) = f(n-1) + f(n-2)
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …
int num = 40;
int[] fibo = {0,1}; // Initial Fibonacci
int i = 0;
println(i, ":", fibo[i]);
for(i = 1; i < num; i++){
println(i, ":", fibo[i]);
fibo = append(fibo, fibo[i-1] + fibo[i]);
}
- append 動的配列の要素を追加する
フィボナッチ数列の可視化
フィボナッチ数を1辺とする正方形を敷き詰めて、長方形を描く。
int[] fibo = {0,1,1};
int[] SGN = {-1, 1, 1, -1}; //敷き詰める方向を決める符号
void setup(){
size(500, 500);
colorMode(HSB, 1);
drawSpiral();
}
void drawSpiral(){
float xPos = 0;
float yPos = 0;
float scalar = (float) width / (2 * fibo[fibo.length - 1]); //拡大・縮小比率
background(0, 0, 1);
translate(width / 2 ,height / 2); //描画ウィンドウ中央に移動
for(int i = 1; i < fibo.length - 1; i++){
fill((0.1 * i) % 1, 1, 1);
//正方形を描く方向を符号の配列に従って変える
rect(scalar * xPos,
scalar * yPos,
scalar * SGN[(i+1) % 4] * fibo[i], //符号が負の場合,逆方向に正方形を描画
scalar * SGN[i % 4] * fibo[i]);
//正方形の位置を符号の配列に従って変える
if (i % 2 == 1){
xPos += SGN[i % 4] * (fibo[i] + fibo[i + 1]);
} else {
yPos += SGN[i % 4] * (fibo[i] + fibo[i + 1]);
}
}
}
- translate 座標を平行移動する。上記の場合は、座標の原点を画面の左上から中央に移動している。
void mouseClicked() {
int nextFibo = fibo[fibo.length-2] + fibo[fibo.length-1];
fibo = append(fibo, nextFibo);
drawSpiral();
println(nextFibo);
}
void draw(){}
フィボナッチらせんを描く関数
void drawSpiral(){
float xPos = 0;
float yPos = 0;
float scalar = (float) width / (2 * fibo[fibo.length-1]); //拡大・縮小比率
background(0, 0, 1);
translate(width / 2 ,height / 2); //描画ウィンドウ中央に移動
for(int i = 1; i < fibo.length - 1; i++){
stroke(0, 0, 0);
rect(scalar * xPos,
scalar * yPos,
scalar * SGN[(i+1) % 4] * fibo[i],
scalar * SGN[i % 4] * fibo[i]);
stroke(0, 1, 1);
arc(scalar * (xPos + SGN[(i+1) % 4] * fibo[i]), //円の中心のx座標
scalar * (yPos + SGN[i % 4] * fibo[i]), //円の中心のy座標
scalar * 2 * fibo[i], //楕円の縦の直径
scalar * 2 * fibo[i], //楕円の横の直径(正円のため縦と同じ)
(1 + i) * PI / 2, //円弧の開始位置(ラジアン)
(2 + i) * PI / 2); //円弧の終了位置
if (i % 2 == 1){
xPos += SGN[i % 4] * (fibo[i] + fibo[i+1]);
} else {
yPos += SGN[i % 4] * (fibo[i] + fibo[i+1]);
}
}
}
らせん
- 自然界のらせん(渦巻き)
- 巻貝の貝殻
- 台風
- 銀河の星の渦
- ひまわりの種の配列
- 座標系
- 3種のらせん
- アルキメデスらせん
- フェルマーらせん
- 対数らせん
- らせんの描画
float theta = 0;
float STEP = 2 * PI * 0.01; //曲線の精度(2*PI = 360度)を100等分
void setup(){
size(500, 500);
}
void draw(){
translate(width / 2, height / 2); //描画ウィンドウの中心に移動
line(rad(theta) * cos(theta), rad(theta) * sin(theta),
rad(theta + STEP) * cos(theta + STEP), rad(theta + STEP) * sin(theta + STEP));
theta += STEP;
}
float rad(float t){ //動径を定める関数
float r = 5 * t; //アルキメデスらせん
//float r = 20 * sqrt(t); //フェルマーらせん
// float r = pow(1.1, t); //対数らせん
return(r);
}
- PIは円周率で3.14159265…
- rad() 角度を度数法から弧度法に変換する。参考サイト
- pow(x,a) べき乗の計算 xのa乗
- sqrt() は平方根
- 自己相似な対数らせん
float STEP = 2 * PI * 0.01; //曲線の精度
void setup(){
size(500, 500);
colorMode(HSB, 1);
}
void draw(){
background(1,0,1);
drawLogSpiral(); //対数らせんを描画
}
void drawLogSpiral(){
float theta = 0;
float scalar = pow(10, (float) mouseX / width) * height / 2;
//マウスのx座標によって1~10倍に拡大する
translate(width / 2, height / 2); //描画ウィンドウの中心に移動
for(int i = 0; i < 2000; i++){
line(scalar * rad(theta) * cos(theta),
scalar * rad(theta) * sin(theta),
scalar * rad(theta + STEP) * cos(theta + STEP),
scalar * rad(theta + STEP) * sin(theta + STEP));
theta -= STEP; //反時計回りに進むほど動径は減少する
}
}
float rad(float t){ //動径を定める関数
float r = pow(1.1, t);
return(r);
}
- mouseX マウスのX座標
再帰的な描画と対数らせん
- ベクトル操作:(x,y)の2つの値を1まとめに扱う。位置や運動を整理して扱うことができる。参考サイト
正方形の中に正方形を再帰的に描く
PVector[] vec; //PVector型の配列を宣言
float gap = 0.01; //内接する正方形のずれ
void setup(){
size(500, 500);
vec = new PVector[4]; //正方形の4つの頂点をベクトルとして生成
vec[0] = new PVector(0, 0); //ウィンドウ左上の角
vec[1] = new PVector(width, 0); //ウィンドウ右上の角
vec[2] = new PVector(width, height); //ウィンドウ右下の角
vec[3] = new PVector(0, height); //ウィンドウ左下の角
}
void draw(){
drawSquare(vec); //4つのベクトルを頂点とする四角形を描画
vec = getVector(vec); //ベクトルをgapの分だけずらす
}
void drawSquare(PVector[] v){
for(int i = 0; i < 4; i++){
line(v[i].x, v[i].y, v[(i + 1) % 4].x, v[(i + 1) % 4].y);
//頂点v[i]と頂点v[i+1]のx座標とy座標の値を取りだし,線分を描く
}
}
PVector[] getVector(PVector[] vec){
PVector[] nextVec = new PVector[4];
for(int i = 0; i < 4; i++){
PVector dir = PVector.sub(vec[(i + 1) % 4], vec[i]); //2頂点間の方向ベクトル
dir.mult(gap); //ずれの分を方向ベクトルにかける
nextVec[i] = PVector.add(vec[i], dir); //元の頂点の位置ベクトルをずらして新たなベクトルを作る
}
return(nextVec);
}
- %は割り算のあまり。9%4=1 (9を4で割るとあまり1)
- 頂点は0,1,2,3なので、3の次は、3+1=4になるが、4で割った余りを考えると4%4=0となる。あまり(剰余系)を使うと、0,1,2,3,0,1,2,3…の循環を表せる。
- v[i].xはベクトルv[i]のx座標
- v[i].yはベクトルv[i]のy座標
- .add(a,b)はベクトルの足し算
- .sub(a,b)はベクトルの引き算
- .mult(a)はベクトルの掛け算
void mouseClicked(){
background(255);
gap = random(1) / 2;
println("gap =", gap);
vec[0] = new PVector(0, 0);
vec[1] = new PVector(width, 0);
vec[2] = new PVector(width, height);
vec[3] = new PVector(0, height);
}
- 多角形に拡張する。
- PVector fromAngle : 指定した角度(ラジアン)の傾きを持つ単位ベクトル(大きさ1)を返す。
PVector[] vec; //PVector型の配列を宣言
float gap = 0.1; //内接する正多角形のずれ
int gon = 8; //正多角形の頂点の数
void setup(){
size(500, 500);
vec = new PVector[gon];
for(int i = 0; i < gon; i++){ //正多角形の頂点の位置ベクトル
vec[i] = PVector.fromAngle(2 * i * PI / gon);
vec[i].mult(width / 2);
}
}
void draw(){
translate(width / 2, height / 2); //描画ウィンドウの中心に移動
drawPolygon(vec);
vec = getVector(vec);
}
void drawPolygon(PVector[] v){
for(int i = 0; i < gon; i++){
line(v[i].x, v[i].y, v[(i + 1) % gon].x, v[(i + 1) % gon].y);
}
}
PVector[] getVector(PVector[] v){
PVector[] nextVec = new PVector[gon];
for(int i = 0; i < gon; i++){
PVector dir = PVector.sub(v[(i + 1) % gon], v[i]);
dir.mult(gap);
nextVec[i] = PVector.add(v[i], dir);
}
return nextVec;
}
void mouseClicked(){
gap = random(1) / 2;
gon = int(random(4, 16));
background(255);
vec = new PVector[gon];
for(int i = 0; i < gon; i++){ //正多角形の頂点の位置ベクトル
vec[i] = PVector.fromAngle(2 * i * PI / gon);
vec[i].mult(width / 2);
}
}
フェルマーらせん
- 離散的らせん
- 回転角
- 有理数
- 1/2,1/3,1/5,1/10,1/20,1/40
- /61
- / 72
- / 17
- / 305
- / 109
- / 360
- 17/55
- 無理数
- sqrt(5)
- 黄金比
- 円周率
- 有理数
int itr = 0; //描画の繰り返し回数
float scalar = 5; //拡大倍率
float rotation;
void setup() {
size(500, 500);
background(255); //背景を白くする
rotation = 17.0 / 55;
// rotation = sqrt(5);
// rotation = (1 + sqrt(5)) / 2;
}
void draw() {
translate(width / 2, height / 2); //描画ウィンドウの中心に移動
fill(0); //点を黒く塗る
drawFermatSpiral(rotation); //引数を回転角とするフェルマーらせんの描画
itr++;
}
void drawFermatSpiral(float rot){
float theta = 2 * PI * itr * rot; //回転角
PVector v = PVector.fromAngle(theta);
v.mult(scalar * sqrt(itr));
ellipse(v.x, v.y, scalar, scalar); //点を描画
}
複数の離散的らせん
int itr = 0; //描画の繰り返し回数
float scalar = 5; //拡大倍率
void setup() {
size(500, 500);
background(255);
}
void draw() {
translate(width / 2, height / 2); //描画ウィンドウの中心に移動
noStroke();
fill(255, 0, 0, 127); //点を赤く塗る
drawFermatSpiral(4.0 / 17);
fill(0, 0, 255, 127); //点を青く塗る
drawFermatSpiral(17.0 / 72);
fill(0, 255, 0, 127); //点を緑に塗る
drawFermatSpiral(72.0 / 305);
itr++;
}
void drawFermatSpiral(float rot){
float theta = 2 * PI * itr * rot; //回転角
PVector v = PVector.fromAngle(theta);
v.mult(scalar * sqrt(itr));
ellipse(v.x, v.y, scalar, scalar); //点を描画
}
セルオートマトン
パスカルの三角形
http://www.xn--u9jtgqbzf1fn77phnzag74e.jp/pascul-nature.html
- 数字を書くプログラム
- textSize() 文字の大きさを決める。
- text(txt,x ,y) txtという文字列を(x,y)に書く。
- splice(配列a,値v, 場所i) 配列aに値vを場所i(先頭からi番目)に挿入します。
int num = 8; //計算する世代数の上限
int[] state = {1}; //初期状態
int gen = 0; //世代
void setup(){
size(500, 500);
}
void draw(){
if(gen < num){
drawNumber(gen); //数字を書く
updateState(); //状態を更新する
}
}
void drawNumber(float y){
float scalar = (float) width / num; // 数字の大きさ
float x = (width - state.length * scalar) * 0.5; // 数字を書く位置のx座標
y *= scalar;
fill(0);
for (int i = 0; i < state.length; i++){
textSize(scalar * 0.5);
text(state[i], x + scalar * 0.5, y + scalar * 0.5);
x += scalar; // 数字を書く位置をx座標方向にずらす
}
}
void updateState(){
int[] BOUNDARY = {0}; //境界値(文字がない所)を0とする
int[] nextState = new int[state.length + 1]; // 次の世代の状態
state = splice(state, BOUNDARY, 0); // 配列の最初に境界値を加える
state = splice(state, BOUNDARY, state.length); // 配列の最後に境界値を加える
for (int i = 0; i < state.length - 1; i++){
nextState[i] = transition(i); // 次世代の状態の計算
}
state = nextState; // 状態を更新
gen++; //世代を1つ増やす
}
int transition(int i){
int nextC = state[i + 1] + state[i]; //パスカルの法則に従った計算
return nextC;
}
- 数値をmodで標記
- mod 割り算のあまり。
- 0,1のパスカルの三角形の遷移ルール
- (0+0) % 2 -> 0
- (0+1) % 2 -> 1
- (1+0) % 2 -> 1
- (1+1) % 2 -> 0
int num = 250;
int mod = 2;
int[] state = {1};
int gen = 0;
void setup(){
size(500, 500);
colorMode(HSB, 1);
background(0, 0, 1);
}
void draw(){
if (gen < num){
drawCell(gen);
updateState();
}
}
void drawCell(float y){
float scalar = (float) width / num; // セルの大きさ
float x = (width - state.length * scalar) * 0.5; // セルのx座標
y *= scalar;
noStroke();
for (int i = 0; i < state.length; i++){
fill(state[i] * 1.0 / mod, state[i] * 1.0 / mod, 1); //色相にセルの状態を割り当て
rect(x, y, scalar, scalar); // セルの描画
x += scalar; // x座標方向にセルをずらす
}
}
void updateState(){
int[] BOUNDARY = {0};
int[] nextState = new int[state.length + 1]; // 次の行の配列
state = splice(state, BOUNDARY, 0); // 配列stateの最初に{0,0}を加える
state = splice(state, BOUNDARY, state.length); // 配列stateの最後に{0,0}を加える
for (int i = 0; i < state.length - 1; i++){
nextState[i] = transition(i); // 次世代のセルの状態の計算
}
state = nextState; // セルの状態を更新
gen++;
}
int transition(int i){
int nextC = (state[i + 1] + state[i]) % mod; // 遷移規則
return nextC;
}
- セルピンスキーのギャスケット
- 0,1のパスカルの三角形の遷移ルール
- 隣接する2つのセルで次の状態が決まる。
- 00 -> 0 or 1
- 01 -> 0 or 1
- 10 -> 0 or 1
- 11 -> 0 or 1
基本セルオートマトン
- 隣接する3つのセルで次の状態が決まる。
- セルの状態は、0,1
- 000 -> 0 or 1
- 001 -> 0 or 1
- 010 -> 0 or 1
- 011 -> 0 or 1
- 100 -> 0 or 1
- 101 -> 0 or 1
- 110 -> 0 or 1
- 111 -> 0 or 1
- 0 or 1 が8通りあるので、合計 2の8乗=256通りのルールがある。
- Wolframは256通りのルールをすべて調べた。
- Elementary Cellular Automaton, Wolfram Math World
- 全て0の00000000(ルール0)から全て1の11111111(ルール255)まで
基本セルオートマトンのソース例
- c(t+1,i) = c(t,i-1) + c(t,i) + c(t,i+1) の例
- 0+0=0, 0+1=0+1=1, 1+1=0 (2進数では10だが、1桁目のみ残す)
- 000 -> 0
- 001 -> 1
- 010 -> 1
- 011 -> 0
- 100 -> 1
- 101 -> 0
- 110 -> 0
- 111 -> 1
int num = 250; //表示する世代数
int mod = 2; //法とする数
int[] state = {1}; //初期状態
int gen = 0;
void setup(){
size(1000, 500);
colorMode(HSB, 1);
background(0, 0, 1);
}
void draw(){
if (gen < num){
drawCell(gen);
updateState();
}
}
void mouseClicked(){
gen = 0;
state = new int[]{1}; //初期状態
mod = int(random(2, 20));
println(mod);
background(0, 0, 1);
}
void drawCell(float y){
float scalar = width * 0.5 / num; // セルの大きさ
float x = (width - state.length * scalar) * 0.5; // セルのx座標
y *= scalar;
noStroke();
for (int i = 0; i < state.length; i++){
fill(state[i] * 1.0 / mod, state[i] * 1.0 / mod, 1); //色相にセルの状態を割り当て
rect(x, y, scalar, scalar); // セルの描画
x += scalar; // x座標方向にセルをずらす
}
}
void updateState(){
int[] BOUNDARY = {0, 0};
int[] nextState = new int[state.length + 2]; // 次の世代の状態
state = splice(state, BOUNDARY, 0); // 配列の最初に境界値を加える
state = splice(state, BOUNDARY, state.length); // 配列の最後に境界値を加える
for (int i = 1; i < state.length - 1; i++){
nextState[i-1] = transition(state[i - 1], state[i], state[i + 1]); // 次世代のセルの状態の計算
}
state = nextState; // セルの状態を更新
gen++; //世代を1つ増やす
}
int transition(int a, int b, int c){
int d = a + b + c; //遷移ルールに従って計算
d = d % mod;
return d;
}
- 遷移ルールに確率的要素を入れる
int transition(int a, int b, int c){
int d;
if (random(1) < 0.999){
d = a + b + c; //99.9%の確率でこのルールを選択
} else {
d = a + c; //0.1%の確率でこのルールを選択
}
d = d % mod;
return d;
}
- マウスクリックするたびに、遷移ルールを変えて描画
int num = 250; //表示する世代数
int mod = 2; //法とする数
int[] state = {1}; //初期状態
int[] rule = {0, 0, 0, 1, 1, 1, 1, 0}; // rule 30 (0011110)
float gen = 0;
void setup(){
size(1000, 500);
colorMode(HSB, 1);
}
void draw(){
if (gen < num){
drawCell(gen);
updateState();
}
}
void mouseClicked(){
gen = 0;
state = new int[]{1}; //初期状態
rule = new int[8];
int ruleInt = 0;
for (int i = 0; i < 8; i++){
rule[i] = int(random(2));
ruleInt += rule[i] * int(pow(2, 7 - i));
}
println(ruleInt);
background(0, 0, 1);
}
void drawCell(float y){
float scalar = width * 0.5 / num; // セルの大きさ
float x = (width - state.length * scalar) * 0.5; // セルのx座標
y *= scalar;
noStroke();
for (int i = 0; i < state.length; i++){
fill(0, 0, 1 - state[i]); //色相にセルの状態を割り当て
rect(x, y, scalar, scalar); // セルの描画
x += scalar; // x座標方向にセルをずらす
}
}
//8個の01要素からなる配列ruleに対して,遷移ルールを決定する
int transition(int a, int b, int c){
int d;
//abcを10進数に置き換える
int ruleInt = int(a * pow(2, 2) + b * pow(2, 1) + c * pow(2, 0));
d = rule[7 - ruleInt];
return d;
}
void updateState(){
int[] BOUNDARY = {0, 0};
int[] nextState = new int[state.length + 2]; // 次の行の配列
state = splice(state, BOUNDARY, 0); // 配列stateの最初に{0,0}を加える
state = splice(state, BOUNDARY, state.length); // 配列stateの最後に{0,0}を加える
for (int i = 1; i < state.length - 1; i++){
nextState[i-1] = transition(state[i - 1], state[i], state[i + 1]); // 次世代のセルの状態の計算
}
state = nextState; // セルの状態を更新
gen++;
}
2次元セルオートマトン
- 正方格子
- 遷移ルールの例
- a
- b c d
- e
next c = a+b+c+d+e mod n
int num = 250; // 行と列の長さ
int mod = 4; // 法とする数
int[][] state = new int[num][num]; // セルの状態を表す行列
void setup(){
size(500, 500);
colorMode(HSB, 1);
initialize(); // 初期化する
frameRate(2); // 0.5秒ごとに遷移
}
void draw(){
drawCell();
updateState();
}
void initialize(){
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
if (i == num / 2 && j == num / 2){
state[i][j] = 1; // 真ん中の成分のみ1
} else {
state[i][j] = 0;
}
}
}
}
void updateState(){
int[][] nextState = new int[num][num]; // 次世代の状態
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
nextState[i][j] = transition(i, j); // 遷移
}
}
state = nextState; //更新
}
int transition(int i, int j){
int nextC;
nextC = state[(i - 1 + num) % num][j] //上のセル
+ state[i][(j - 1 + num) % num] //左のセル
+ state[i][j] //中央のセル
+ state[i][(j + 1) % num] //右のセル
+ state[(i + 1) % num][j]; //下のセル
nextC = nextC % mod;
return nextC;
}
void drawCell(){
float scalar = (float) height / num; // セルのサイズ
float y = 0; // セルのy座標
float x;
for (int i = 0; i < num; i++){
x = 0; // セルのx座標
for (int j = 0; j < num; j++){
noStroke();
fill(state[i][j] * 1.0 / mod, state[i][j] * 1.0 / mod, 1); // セルの色
rect(x, y, scalar, scalar);
x += scalar;
}
y += scalar;
}
}
ライフゲーム
- 遷移ルール
- セルの状態は、生(1)か死(0)か
- セルが1の場合
- 自分の周りに1が2個か3個の場合、1
- それ以外の場合、0
- セルが0の場合
- 自分の周りに1が3個の場合、1
- それ以外の場合、0
- 初期化
- ランダムに生と死を配置
- num = 50;
- mod = 1;
- frameRate(4);
void initialize(){
float r;
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
r = random(100);
if ( r > 85 ){
state[i][j] = 1;
} else {
state[i][j] = 0;
}
}
}
}
- 遷移ルール
int transition(int i, int j){
int aroundC;
int nextC = 0;
aroundC =
state[(i - 1 + num) % num][j] //上のセル
+ state[(i - 1 + num) % num][(j - 1 + num) % num] //上のセル
+ state[(i - 1 + num) % num][(j + 1) % num] //上のセル
+ state[i][(j - 1 + num) % num] //左のセル
+ state[i][(j + 1) % num] //右のセル
+ state[(i + 1) % num][(j - 1 + num) % num] //下のセル
+ state[(i + 1) % num][j] //下のセル
+ state[(i + 1) % num][(j + 1) % num]; //下のセル
if(state[i][j] == 1){
if(aroundC == 2 || aroundC == 3) {
nextC = 1;
}
else{
nextC = 0;
}
}
if(state[i][j] == 0){
if(aroundC == 3) {
nextC = 1;
}
else{
nextC = 0;
}
}
return nextC;
}
void drawCell(){
float scalar = (float) height / num; // セルのサイズ
float y = 0; // セルのy座標
float x;
for (int i = 0; i < num; i++){
x = 0; // セルのx座標
for (int j = 0; j < num; j++){
noStroke();
fill(state[i][j] * 1.0, state[i][j] * 1.0, 1); // セルの色
rect(x, y, scalar, scalar);
x += scalar;
}
y += scalar;
}
}
正六角形セルオートマトン
- 六角格子
ベクトルPVectorクラスを使った図形描画PShapeで六角格子を作る。
- beginShape()とendShape()の間にvertex()で頂点を並べて、図形を描く。vertexについて解説
- createShape()で図形を作成して、再利用する。
PVector[][] lattice;
PShape tile;
PVector[] base = new PVector[2]; //格子を張るベクトル
int num = 100; //描画する格子の行数
float scalar;
int[][] state = new int[num][num]; //セルの状態を表す行列
int mod = 10; //法とする数
void setup(){
size(600, 800);
colorMode(HSB, 1);
scalar = height * 1.0 / num; //ウィンドウと格子の行数から格子の大きさを決定
initialize(); // 初期状態
makeHexVector(); //六角格子を張るベクトルの生成
makeLattice(); //格子点ベクトルを生成
makeHex(); //正六角形タイルを生成
drawTiling(); //タイリングを描画
frameRate(2);
}
void draw(){
background(0, 0, 1);
int[][] nextState = new int[num][num]; //次世代の行列
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
nextState[i][j] = transition(i, j); //遷移
}
}
state = nextState; //状態を更新
drawTiling();
}
void initialize(){
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
if (i == num / 2 && j == num / 2){
state[i][j] = 1; // 中央の成分のみ1
} else {
state[i][j] = 0;
}
}
}
}
//六角格子を張るベクトルを作る。
//円周上の時計回りに90度(PI/2)と30度(PI/6)に点を取ってベクトルを作る。
void makeHexVector(){
base[0] = PVector.fromAngle(PI/2);
base[1] = PVector.fromAngle(PI/6);
}
//ウィンドウ内に収まるように格子点の配列latticeを定める。
//ウィンドウからはみ出た格子点は%(余り)演算でウィンドウ上部に戻す。
void makeLattice(){
lattice = new PVector[num][num];
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
PVector v = PVector.mult(base[0], i * scalar);
v.add(PVector.mult(base[1], j * scalar));
lattice[i][j] = new PVector(v.x, v.y % height);
}
}
}
//fromAngleで60度(PI/3)刻みで正6角形の格子を作る
//
void makeHex(){
tile = createShape();
tile.beginShape();
tile.noStroke();
for (int i = 0; i < 6; i++){
PVector v = PVector.fromAngle(2 * PI * i / 6);
v.mult(scalar / sqrt(3));
tile.vertex(v.x, v.y);
}
tile.endShape(CLOSE);
}
//makeHex関数で作った正6角形の格子に沿って配置する。
void drawTiling(){
for (int i = 0; i < num; i++){
for (int j = 0; j < num; j++){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); //タイルの位置を指定
setTileColor(tile, i, j);
shape(tile); //タイルを描画
}
}
}
void setTileColor(PShape t, int i, int j){
t.setFill(color(state[i][j] * 1.0 / mod, state[i][j] * 1.0 / mod, 1));
}
int transition(int i, int j){
int d;
d = state[i][j] //中央のセル
+ state[(i - 1 + num) % num][j] //上のセル
+ state[(i - 1 + num) % num][(j + 1) % num] //右上のセル
+ state[i][(j + 1) % num] //右下のセル
+ state[(i + 1) % num][j] //下のセル
+ state[(i + 1) % num][(j - 1 + num) % num] //左下のセル
+ state[i][(j - 1 + num) % num]; //左上のセル
d = d % mod;
return d;
}
セルオートマトン資料
- ライフゲームのWindowsソフト /
- Cellular Automata explorer
- Wolfram Math World Game of Life
- HashLife
- http://golly.sourceforge.net/
- セルオートマトン音楽
- WolframTones
- Life Game Orchestra : Doccument / YouTube
- 参考
ワイヤワールド /
人工生命
ラングトンのアリ
ラングトンのアリ /
平面が格子状に構成され、各マスが白または黒で塗られる。 アリは各ステップで上下左右のいずれかのマスに移動することができる。アリは以下の規則に従って移動する。
- 白いマスにアリがいた場合、90°右に方向転換し、そのマスの色を反転させ、1マス前進する。
- 黒いマスにアリがいた場合、90°左に方向転換し、そのマスの色を反転させ、1マス前進する。
この単純な規則で驚くほど複雑な動作をする。
ソース例
参考 ラングトンの蟻 Processing / tado Langton's ant /
- boolean型の変数の値は、true か falseの2値
- この場合は、cellsの色が、黒(true)か白(false)かの2値
- ! 演算子は、NOT(否定)で、!(true)はfalseのことで !(false)はtrueになる。
- 輪郭の色の指定はstroke()、塗りつぶしの色の指定は fill()
- アリの座標は、PVector型のantで表す。
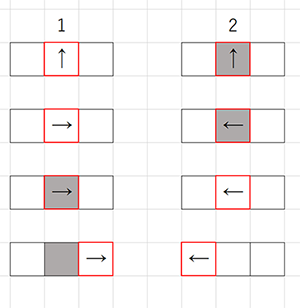
- アリの進行方向は、ant_directionで表す。0(上),1(右),2(下),3(左)の4方向。
- turn rightは現在の方向に1足した値の4で割った余り。
- (ant_direction + 1) % 4; 例: 2(下)のとき、turn rightで2+1=3(左)
- turn leftは現在の方向に3足した値の4で割った余り。
- (ant_direction + 3) % 4; 例: 2(下)のとき、turn leftで(2+3)%4=1(右)
- turn rightは現在の方向に1足した値の4で割った余り。
- 初期状態 initialize_cells()
- 0 すべて 白 :しばらく彷徨った後、行進する。
- 1 すべて 黒:しばらく彷徨った後、行進する。
- 2 中央に黒い長方形 :長方形の周囲に城壁を築く。その後、行進する。
- 3 ランダム :
int CELL_NUM = 100;
int CELL_SIZE = 5;
boolean[][] cells = new boolean[CELL_NUM][CELL_NUM];
PVector ant;
int ant_direction; // 0=up, 1=right, 2=down, 3=left
void settings() {
size(CELL_NUM * CELL_SIZE, CELL_NUM * CELL_SIZE);
}
void setup(){
// initialize cells, 0: all white, 1: all black, 2: put black rectangle, 3: random
initialize_cells(0);
// initialize ant position
ant = new PVector(int(CELL_NUM / 2),int(CELL_NUM / 2));
ant_direction = 0;
}
void draw(){
// clear screen
fill(255);
rect(0, 0, width, height);
// draw cells
noStroke();
fill(30);
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
if(cells[w][h] == true){
rect(w * CELL_SIZE, h * CELL_SIZE, CELL_SIZE, CELL_SIZE);
}
}
}
// draw lines
stroke(128);
strokeWeight(1);
for(int i = 0; i < CELL_NUM; i++){
line(i * CELL_SIZE, 0, i * CELL_SIZE, height);
line(0, i * CELL_SIZE, width, i * CELL_SIZE);
}
// draw ant
fill(255, 0, 0);
rect(ant.x * CELL_SIZE, ant.y * CELL_SIZE, CELL_SIZE, CELL_SIZE);
//act ant
act_ant();
}
void act_ant(){
if(cells[(int)ant.x][(int)ant.y] == true){
ant_direction = (ant_direction + 3) % 4; // turn left
}else {
ant_direction = (ant_direction + 1) % 4; // turn right
}
cells[(int)ant.x][(int)ant.y] = !cells[(int)ant.x][(int)ant.y];
forward_ant();
}
void forward_ant(){
switch(ant_direction){
case 0:
ant.y = (ant.y - 1 + CELL_NUM) % CELL_NUM;
break;
case 1:
ant.x = (ant.x + 1) % CELL_NUM;
break;
case 2:
ant.y = (ant.y + 1) % CELL_NUM;
break;
case 3:
ant.x = (ant.x - 1 + CELL_NUM) % CELL_NUM;
break;
}
}
void initialize_cells(int method){
switch(method){
case 0: // all white
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = false;
}
}
break;
case 1: // all black
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = true;
}
}
break;
case 2: // put black rectangle
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = false;
}
}
int rect_x = 40;
int rect_y = 20;
for(int w = (CELL_NUM / 2) - int(rect_x / 2); w < (CELL_NUM / 2) + int(rect_x / 2); w++){
for(int h = (CELL_NUM / 2) - int(rect_y / 2); h < (CELL_NUM / 2) + int(rect_y / 2); h++){
cells[w][h] = true;
}
}
break;
case 3: // random
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
if(random(10) > 5){
cells[w][h] = true;
}else{
cells[w][h] = false;
}
}
}
break;
}
}
ラングトンのアリの拡張
多数の色を使うように拡張する。色の変化は、循環となり、アリの動きは各色ごとに右か左に向きを変えて1マス進むことになる。これを色の順に L(左)と R(右)を並べて表す。
- 以下のソース例
- mod = 4で、4の剰余系(0,1,2,3)で色を表す
- 色はHSB系で表す。H:色相、S:彩度、B:明度
- この例では、colorMode(HSB, mod, 100, 100)として、色相(mod=)4段階、彩度100段階、明度100段階で表す。
- 参考:色彩
- 各色(0123)による進路「LRLR」の時、彷徨った後、行進する(通常のラングトンのアリ)。
- 各色(0123)による進路「RLLR」の時、正方形を描きながら彷徨う。
- 以下のソース例は「RLLR」としている。
int CELL_NUM = 100;
int CELL_SIZE = 5;
int[][] cells = new int[CELL_NUM][CELL_NUM];
int mod = 4;
PVector ant;
int ant_direction; // 0=up, 1=right, 2=down, 3=left
void settings() {
size(CELL_NUM * CELL_SIZE, CELL_NUM * CELL_SIZE);
}
void setup(){
// initialize cells, 0: all white, 1: all black, 2: put rectangle, 3:random
colorMode(HSB, mod, 100, 100);
initialize_cells(0);
// initialize ant position
ant = new PVector(int(CELL_NUM / 2),int(CELL_NUM / 2));
ant_direction = 0;
}
void draw(){
// clear screen
fill(0,0,95);
rect(0, 0, width, height);
// draw cells
noStroke();
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
if(cells[w][h] > 0){
fill(cells[w][h], 75, 75); // セルの色
rect(w * CELL_SIZE, h * CELL_SIZE, CELL_SIZE, CELL_SIZE);
}
}
}
// draw lines
stroke(0,0,90);
strokeWeight(1);
for(int i = 0; i < CELL_NUM; i++){
line(i * CELL_SIZE, 0, i * CELL_SIZE, height);
line(0, i * CELL_SIZE, width, i * CELL_SIZE);
}
// draw ant
fill(0, 100, 100);
rect(ant.x * CELL_SIZE, ant.y * CELL_SIZE, CELL_SIZE, CELL_SIZE);
//act ant
act_ant();
}
void act_ant(){
switch(cells[(int)ant.x][(int)ant.y]){
// RLLR
case 0:
ant_direction = (ant_direction + 1) % 4; // turn right
break;
case 1:
ant_direction = (ant_direction + 3) % 4; // turn left
break;
case 2:
ant_direction = (ant_direction + 3) % 4; // turn left
break;
case 3:
ant_direction = (ant_direction + 1) % 4; // turn right
break;
}
cells[(int)ant.x][(int)ant.y] = ( cells[(int)ant.x][(int)ant.y] + 1 ) % mod;
forward_ant();
}
void forward_ant(){
switch(ant_direction){
case 0:
ant.y = (ant.y - 1 + CELL_NUM) % CELL_NUM;
break;
case 1:
ant.x = (ant.x + 1) % CELL_NUM;
break;
case 2:
ant.y = (ant.y + 1) % CELL_NUM;
break;
case 3:
ant.x = (ant.x - 1 + CELL_NUM) % CELL_NUM;
break;
}
}
void initialize_cells(int method){
switch(method){
case 0: // all white
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = 0;
}
}
break;
case 1: // all black
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = mod/2;
}
}
break;
case 2: // put black rectangle
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = 0;
}
}
int rect_x = 40;
int rect_y = 20;
for(int w = (CELL_NUM / 2) - int(rect_x / 2); w < (CELL_NUM / 2) + int(rect_x / 2); w++){
for(int h = (CELL_NUM / 2) - int(rect_y / 2); h < (CELL_NUM / 2) + int(rect_y / 2); h++){
cells[w][h] = mod/2;
}
}
break;
case 3: // random
for(int w = 0; w < CELL_NUM; w++){
for(int h = 0; h < CELL_NUM; h++){
cells[w][h] = (int)random(mod);
}
}
break;
}
}
レイノルズのボイド
ボイド(Boids)は、クレイグ・レイノルズが考案・作製した人工生命シミュレーションプログラムである。名称は「鳥もどき(bird-oid)」から取られている。コンピュータ上の鳥オブジェクトに以下の三つの動作規則を与え、多数を同時に動かして群れの振る舞いをシミュレーションする。
- 分離(Separation)
- 鳥オブジェクトが他の鳥オブジェクトとぶつからないように距離をとる。
- 整列(Alignment)
- 鳥オブジェクトが他の鳥オブジェクトと概ね同じ方向に飛ぶように速度と方向を合わせる。
- 結合(Cohesion)
- 鳥オブジェクトが他の鳥オブジェクトが集まっている群れの中心方向へ向かうように方向を変える。
驚くほど自然な動きを見せ、単純な規則を用いて群としての複雑な振る舞いを再現できる。
ボイド wiki / Reynolds Boids Reynolds official /
Processing公式サイトのソース例
- Birds Algorhythm Craig Reynolds Processing official /
注)一部改変
- TWO_PI 3.1415...(円周率)×2のこと
- Pvector.normalize() ベクトルの大きさを1にする。
- pushMatrix(), translate(x,y);rotate(theta);beginShape();vertex();endShape();popMatrix();を使った鳥(三角形)の描画
- クラスの設計
- Flock 鳥の群れ:Boidオブジェクトのリスト()
- Boid 1羽の鳥
- separate() 分離の加速度を計算
- 距離がdesiredseparationの値より小さいと近すぎるとみなし、分離しようとする。
- align() 整列の加速度を計算
- 距離がneighbordistの値より小さいと近傍(群れの仲間)とみなし、整列しようとする。群れの平均速度(速さと方向)に合わせようとする。
- cohesion() 結合の加速度を計算
- 距離がneighbordistの値より小さいと近傍(群れの仲間)とみなし、結合しようとする。群れの中心に向かおうとする。
- seek(PVector target) targetを追跡(seek)する加速度の計算
- separate() 分離の加速度を計算
Flock flock;
void setup() {
size(640, 360);
flock = new Flock();
// Add an initial set of boids into the system
for (int i = 0; i < 150; i++) {
flock.addBoid(new Boid(width/2,height/2));
}
}
void draw() {
background(50);
flock.run();
}
// Add a new boid into the System
void mousePressed() {
flock.addBoid(new Boid(mouseX,mouseY));
}
// The Flock (a list of Boid objects)
class Flock {
ArrayList<Boid> boids; // An ArrayList for all the boids
Flock() {
boids = new ArrayList<Boid>(); // Initialize the ArrayList
}
void run() {
for (Boid b : boids) {
b.run(boids); // Passing the entire list of boids to each boid individually
}
}
void addBoid(Boid b) {
boids.add(b);
}
}
// The Boid class
class Boid {
PVector position;
PVector velocity;
PVector acceleration;
float r; // Bird size
float maxforce; // Maximum steering force
float maxspeed; // Maximum speed
Boid(float x, float y) {
acceleration = new PVector(0, 0);
float angle = random(TWO_PI);
velocity = new PVector(cos(angle), sin(angle));
position = new PVector(x, y);
r = 2.0;
maxspeed = 2;
maxforce = 0.03;
}
void run(ArrayList<Boid> boids) {
flock(boids);
update();
borders();
render();
}
void applyForce(PVector force) {
// We could add mass here if we want A = F / M
acceleration.add(force);
}
// We accumulate a new acceleration each time based on three rules
void flock(ArrayList<Boid> boids) {
PVector sep = separate(boids); // Separation
PVector ali = align(boids); // Alignment
PVector coh = cohesion(boids); // Cohesion
// Arbitrarily weight these forces
sep.mult(1.5);
ali.mult(1.0);
coh.mult(1.0);
// Add the force vectors to acceleration
applyForce(sep);
applyForce(ali);
applyForce(coh);
}
// Method to update position
void update() {
// Update velocity
velocity.add(acceleration);
// Limit speed
velocity.limit(maxspeed);
position.add(velocity);
// Reset accelertion to 0 each cycle
acceleration.mult(0);
}
// A method that calculates and applies a steering force towards a target
// STEER = DESIRED MINUS VELOCITY
PVector seek(PVector target) {
PVector desired = PVector.sub(target, position); // A vector pointing from the position to the target
// Scale to maximum speed
desired.normalize();
desired.mult(maxspeed);
// Steering = Desired minus Velocity
PVector steer = PVector.sub(desired, velocity);
steer.limit(maxforce); // Limit to maximum steering force
return steer;
}
void render() {
// Draw a triangle rotated in the direction of velocity
float theta = velocity.heading2D() + radians(90);
// heading2D() above is now heading() but leaving old syntax until Processing.js catches up
fill(200, 100);
stroke(255);
pushMatrix();
translate(position.x, position.y);
rotate(theta);
beginShape(TRIANGLES);
vertex(0, -r*2);
vertex(-r, r*2);
vertex(r, r*2);
endShape();
popMatrix();
}
// Wraparound
void borders() {
if (position.x < -r) position.x = width+r;
if (position.y < -r) position.y = height+r;
if (position.x > width+r) position.x = -r;
if (position.y > height+r) position.y = -r;
}
// Separation
// Method checks for nearby boids and steers away
PVector separate (ArrayList<Boid> boids) {
float desiredseparation = 25.0f;
PVector steer = new PVector(0, 0, 0);
int count = 0;
// For every boid in the system, check if it's too close
for (Boid other : boids) {
float d = PVector.dist(position, other.position);
// If the distance is greater than 0 and less than an arbitrary amount (0 when you are yourself)
if ((d > 0) && (d < desiredseparation)) {
// Calculate vector pointing away from neighbor
PVector diff = PVector.sub(position, other.position);
diff.normalize();
diff.div(d); // Weight by distance
steer.add(diff);
count++; // Keep track of how many
}
}
// Average -- divide by how many
if (count > 0) {
steer.div((float)count);
}
// As long as the vector is greater than 0
if (steer.mag() > 0) {
// First two lines of code below could be condensed with new PVector setMag() method
// Not using this method until Processing.js catches up
// steer.setMag(maxspeed);
// Implement Reynolds: Steering = Desired - Velocity
steer.normalize();
steer.mult(maxspeed);
steer.sub(velocity);
steer.limit(maxforce);
}
return steer;
}
// Alignment
// For every nearby boid in the system, calculate the average velocity
PVector align (ArrayList<Boid> boids) {
float neighbordist = 50;
PVector sum = new PVector(0, 0);
int count = 0;
for (Boid other : boids) {
float d = PVector.dist(position, other.position);
if ((d > 0) && (d < neighbordist)) {
sum.add(other.velocity);
count++;
}
}
if (count > 0) {
sum.div((float)count);
// First two lines of code below could be condensed with new PVector setMag() method
// Not using this method until Processing.js catches up
// sum.setMag(maxspeed);
// Implement Reynolds: Steering = Desired - Velocity
sum.normalize();
sum.mult(maxspeed);
PVector steer = PVector.sub(sum, velocity);
steer.limit(maxforce);
return steer;
}
else {
return new PVector(0, 0);
}
}
// Cohesion
// For the average position (i.e. center) of all nearby boids, calculate steering vector towards that position
PVector cohesion (ArrayList<Boid> boids) {
float neighbordist = 50;
PVector sum = new PVector(0, 0); // Start with empty vector to accumulate all positions
int count = 0;
for (Boid other : boids) {
float d = PVector.dist(position, other.position);
if ((d > 0) && (d < neighbordist)) {
sum.add(other.position); // Add position
count++;
}
}
if (count > 0) {
sum.div(count);
return seek(sum); // Steer towards the position
}
else {
return new PVector(0, 0);
}
}
}
クラスを使わない簡略化したソース例
クラスの設計やPVectorを使用していない例である。簡潔に記述されている。
https://garchiving.com/algorithm-of-boids-with-processing/
int num = 80;
float[] x =new float[num];
float[] y =new float[num];
float[] r =new float[num];
float[] dx =new float[num];
float[] dy =new float[num];
float[] ctrDirX =new float[num];
float[] ctrDirY =new float[num];
float[] vel =new float[num];
float[] velAngle =new float[num];
float[] contX =new float[num];
float[] contY =new float[num];
float[] kX =new float[num];
float[] kY =new float[num];
float aveX, aveY, aveAngle, aveVel;
float velX, velY;
void setup() {
for (int i=0; i<num; i++) {
r[i] = 10;
x[i] = 250+80*cos(radians((360/num)*i));
y[i] = 250+80*sin(radians((360/num)*i));
velAngle[i] = (360/num)*i;
vel[i] = random(0, 5.5);
dx[i] = vel[i]*cos(radians(velAngle[i]));
dy[i] = vel[i]*sin(radians(velAngle[i]));
}
size(800, 800);
background(240);
smooth();
}
void draw() {
background(240);
stroke(100);
strokeWeight(1);
noFill();
for (int i=0; i<num; i++) {
ellipse(x[i], y[i], 10, 10);
line(x[i], y[i], x[i]+10*dx[i], y[i]+10*dy[i]);
}
aveX = 0;
aveY = 0;
for (int i=0; i<num; i++) {
aveX += x[i];
aveY += y[i];
}
aveX /= num;
aveY /= num;
if (mousePressed == true) {
aveX = mouseX;
aveY = mouseY;
stroke(0, 0, 255);
fill(0, 0, 255);
ellipse(aveX, aveY, 10, 10);
}
for (int i=0; i<num; i++) {
ctrDirX[i] = aveX - x[i];
ctrDirY[i] = aveY - y[i];
}
aveVel = 0;
aveAngle = 0;
for (int i=0; i<num; i++) {
aveVel += sqrt(dx[i]*dx[i]+dy[i]*dy[i]);
aveAngle += degrees(atan2(dy[i], dx[i]));
}
aveVel /= num;
aveAngle /= num;
velX = aveVel*cos(radians(aveAngle));
velY = aveVel*sin(radians(aveAngle));
for (int i=0; i<num; i++) {
contX[i]=0;
contY[i]=0;
for (int j=0; j<num; j++) {
if (i!=j) {
float dist=sqrt((x[j]-x[i])*(x[j]-x[i])+(y[j]-y[i])*(y[j]-y[i]));
if (0<dist&&dist<15) {
contX[i] = -1*(x[j]-x[i]);
contY[i] = -1*(y[j]-y[i]);
float temp = sqrt(contX[i]*contX[i]+contY[i]*contY[i]);
contX[i]/=temp;
contY[i]/=temp;
}
}
}
}
for (int i=0; i<num; i++) {
kX[i] = 0.03*ctrDirX[i]+4.0*velX+5.0*contX[i];
kY[i] = 0.03*ctrDirY[i]+4.0*velY+5.0*contY[i];
float tempVel = sqrt(kX[i]*kX[i]+kY[i]*kY[i]);
if (tempVel>2) {
kX[i]=2*kX[i]/tempVel;
kY[i]=2*kY[i]/tempVel;
}
dx[i] += (kX[i]-dx[i])*0.02;
dy[i] += (kY[i]-dy[i])*0.02;
x[i] += dx[i];
y[i] += dy[i];
x[i] = x[i] % width;
y[i] = y[i] % height;
}
}
Gray-Scott Reaction-Diffusion(反応拡散系)モデル
2変数の連立偏微分方程式を考える。
- https://www.karlsims.com/rd.html
- https://mrob.com/pub/comp/xmorphia/ogl/index.html
- http://pmneila.github.io/jsexp/grayscott/
- https://github.com/MStrandh/gray_scott_reaction_diffusion
- https://github.com/Nekodigi/Reaction-Diffusion-Algorithm
int M = 640;
int N = 480;
//System parameters
double diffU;
double diffV;
double paramF;
double paramK;
boolean rndInitCondition;
double[][] U = new double[M][N];
double[][] V = new double[M][N];
double[][] dU = new double[M][N];
double[][] dV = new double[M][N];
//int[][] offset = new int[N][2];
void settings() {
size(M,N);
}
void generateInitialState() {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
U[i][j] = 1.0;
V[i][j] = 0.0;
}
}
if (rndInitCondition) {
for (int i = M/3; i < 2*M/3; i++) {
for (int j = N/3; j < 2*N/3; j++) {
U[i][j] = 0.5*(1 + random(-1, 1));
V[i][j] = 0.25*( 1 + random(-1, 1));
}
}
} else {
for (int i = M/3; i < 2*M/3; i++) {
for (int j = N/3; j < 2*N/3; j++) {
U[i][j] = 0.5;
V[i][j] = 0.25;
}
}
}
}
void setup() {
frameRate(48);
smooth();
colorMode(HSB,1.0);
//Set default parameters;
diffU = 0.16;
diffV = 0.08;
paramF = 0.035;
paramK = 0.06;
rndInitCondition = true;
//Populate U and V with initial data
generateInitialState();
}
void timestep(double F, double K, double diffU, double diffV) {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
int p = i + j*N;
double u = U[i][j];
double v = V[i][j];
double uvv = u*v*v;
int left = (i-1+M) % M;
int right = (i+1) % M;
int up = (j-1+N) % N;
int down = (j+1) % N;
double lapU = (U[left][j] + U[right][j] + U[i][up] + U[i][down] - 4*u);
double lapV = (V[left][j] + V[right][j] + V[i][up] + V[i][down] - 4*v);
dU[i][j] = diffU*lapU - uvv + F*(1 - u);
dV[i][j] = diffV*lapV + uvv - (K+F)*v;
}
}
for (int i= 0; i < M; i++) {
for (int j = 0; j < N; j++){
U[i][j] += dU[i][j];
V[i][j] += dV[i][j];
}
}
}
void draw(){
for (int k = 0; k < 10; k++) {
timestep(paramF, paramK, diffU, diffV);
}
// Draw points
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
set(i, j, color((float)(1-U[i][j]),0.9, 0.5 ));
// set(i, j, color(0.74, 0.87, (float)(1-U[i][j])));
// set(i, j, color(0.5, 0.6, (float)(V[i][j])));
}
}
}
void keyPressed() {
switch (key) {
case '1':
diffU = 0.16;
diffV = 0.08;
paramF = 0.035;
paramK = 0.06;
generateInitialState();
break;
case '2':
diffU = 0.16;
diffV = 0.08;
paramF = 0.042;
paramK = 0.065;
generateInitialState();
break;
case '3':
diffU = 0.18;
diffV = 0.13;
paramF = 0.025;
paramK = 0.056;
generateInitialState();
break;
case '4':
diffU = 0.18;
diffV = 0.09;
paramF = 0.02;
paramK = 0.056;
generateInitialState();
break;
case '5':
diffU = 0.14;
diffV = 0.06;
paramF = 0.035;
paramK = 0.065;
generateInitialState();
break;
case '6':
diffU = 0.19;
diffV = 0.09;
paramF = 0.062;
paramK = 0.062;
generateInitialState();
break;
case '7':
diffU = 0.16;
diffV = 0.08;
paramF = 0.05;
paramK = 0.065;
generateInitialState();
break;
case 'r':
rndInitCondition = true;
generateInitialState();
break;
case 'n':
rndInitCondition = false;
generateInitialState();
}
}
Neural Networks
- 神経回路モデル(PPT)
- 神経細胞の写真,構成図[ 1 | 2 | 3 ]
- Perceptron,
- Back Propagation
- Hopfield Network
- 自己組織化ネットワーク
- 脳の潜在能力
- 天文学者カール・セーガン「人間の脳はおよそ2,000万冊,すなわち世界最大の図書館に収められているのと同じ数の本を満たすほどの情報を収納することができる」
- 神経科学者「人は平均寿命の間に脳の潜在能力の0.01%(0.0001)しか使っていない」
Neural Networkのしくみを知る
- 学習データの準備
- お手本となる数百件〜数十万件のデータを人間が集めて準備しておく
- Neural Networkのモデルの学習
- 学習データに含まれるパターンを抽出する
- モデルの利用
- 学習済みのモデルを分類や予測に利用する
- 例 身長、体重を元に大人か子供か判別する
- 今までは、判別の計算式を人間がやっていた
- Neural Networkではコンピュータが重み付けを行う
- 間違いが少なくなるように重み付けを変えていく
- Tensorflow Playgroundのデモ
- 例 経度と緯度から街の内側か外側かを分類する
- 線を引いて判別できない
- ニューラルネットワークの階層化(隠れ層の追加)が必要
- Tensorflow Playgroundのデモ
- 例 縦位置と横位置で並んだ子供を分類する
- ニューロンの数を増やしたり階層を深くすることで賢くなる
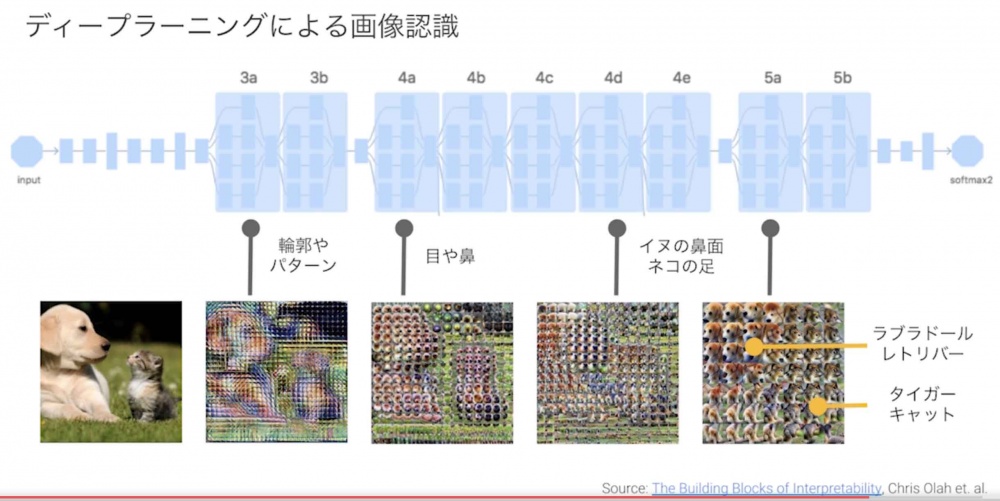
- 3段以上の深い階層を持つニューラルネットワークをディープラーニングと言う
- Tensorflow Playgroundのデモ
Genetic Algorithm
- カール・セーガン「コスモス」エピソードII第3話「平家物語と蟹のなぞ」
- GAの概念と応用例
oFサンプル集
ランダムウォーク
1次元セルオートマトン
ライフゲーム
ラングトンのアリ
Boid
物理エンジン Box2D
自己相似形
P5サンプル集
音に反応する円
minimライブラリーをインストールする。
/**
* Circles responding Sound Level
*/
import ddf.minim.spi.*;
import ddf.minim.signals.*;
import ddf.minim.*;
import ddf.minim.analysis.*;
import ddf.minim.ugens.*;
import ddf.minim.effects.*;
Minim minim;
AudioInput in;
void setup(){
size(500, 500);
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, 512);
background(0);
}
void draw(){
colorMode(RGB, 255);
fill(0, 150);
rect(-1, -1, width, height);
colorMode(HSB, 360, 100, 100);
float brightness = 50 + map(in.mix.level(), 0, 0.5, 0, 50);
float hue = map(in.mix.level(), 0, 0.7, 0, 360);
fill(hue, 100, brightness);
float radious = 50 + map(in.mix.level(), 0, 0.5, 0, 100);
int x = 250;
int y = 250;
ellipse( x, y, radious *2, radious * 2);
}
void stop(){
in.close();
minim.stop();
super.stop();
}
カメラ入力
Video|GStreamer-based video library for Processingライブラリをインストール。
- 使用可能なカメラのリスト出力
import processing.video.*;
void setup(){
size(320, 240);
String[] cameras = Capture.list();
for(int i=0; i<cameras.length; i++){
println("[" + i + "] " + cameras[i]);
}
}
- カメラ画像の出力
import processing.video.*;
Capture cam;
void setup(){
size(640, 480);
String[] cameras = Capture.list();
for(int i=0; i<cameras.length; i++){
println("[" + i + "] " + cameras[i]);
}
cam = new Capture(this, cameras[1]);
cam.start();
}
void draw(){
if(cam.available() == true){
cam.read();
}
image(cam, 0, 0);
}
- 差分から動きを検出
import processing.video.*;
int numPixels;
int[] previousFrame;
int noiseFilter = 50;
Capture video;
void setup() {
size(640, 480);
video = new Capture(this, width, height, 30);
video.start();
numPixels = video.width * video.height;
previousFrame = new int[numPixels];
loadPixels();
}
void draw() {
if (video.available()) {
video.read();
video.loadPixels();
int movementSum = 0;
for (int i = 0; i < numPixels; i++) {
color currColor = video.pixels[i];
color prevColor = previousFrame[i];
//R, G, B
int currR = (currColor >> 16) & 0xFF;
int currG = (currColor >> 8) & 0xFF;
int currB = currColor & 0xFF;
//
int prevR = (prevColor >> 16) & 0xFF;
int prevG = (prevColor >> 8) & 0xFF;
int prevB = prevColor & 0xFF;
//
int diffR = abs(currR - prevR);
int diffG = abs(currG - prevG);
int diffB = abs(currB - prevB);
//noiseFilter
if (diffR + diffG + diffB > noiseFilter) {
movementSum ++;
pixels[i] = color(currR, currG, currB);
//
//pixels[i] = 0xFF000000 | (currR << 16) | (currG << 8) | currB;
} else {
pixels[i] = color(0);
}
//
previousFrame[i] = currColor;
}
updatePixels(); //
println(movementSum); //
}
}
引力と加速度
「Nature of Code」第1章の「1.10 Interactivity with Acceleration」(p57)より。(一部改変)pdf
- 粒子はマウスポインタに引力で引き付けられれ、軌跡を残しながらマウスに近づく。
- 引力は、距離が近いほど、強くなる(反比例)。
- 速度には上限(topspeed)があり、引力と粒子の運動量(速度)が釣り合うと、マウスのまわりを回る惑星のような動きになる。
- Moverクラスの作成
- ベクトルPVectorを使い、location(位置)、velocity(速度)、acceleration(加速度)定義し、力学運動を記述している。
- 速度は、現在速度に加速度を加算 velocity.add(acceleration);
- 位置は、現在位置に速を加算 location.add(velocity);
Mover[] movers = new Mover[1000];//An array of objects
void setup() {
size(1000, 1000);
smooth();
background(0);
for (int i = 0; i < movers.length; i++) {
movers[i] = new Mover();// Initialize each object in the array.
}
}
void draw() {
// background(0);
fill(0,40);
rect(0,0,width,height);
for (int i = 0; i < movers.length; i++) {
//Calling functions on all the objects in the array
movers[i].update();
movers[i].checkEdges();
movers[i].display();
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float topspeed;
Mover() {
location = new PVector(random(width), random(height));
velocity = new PVector(0, 0);
topspeed = 4.5;
}
void update() {
//Our algorithm for calculating acceleration:
//Find the vector pointing towards the mouse.
PVector mouse = new PVector(mouseX, mouseY);
PVector dir = PVector.sub(mouse, location);
float magn = dir.mag();
dir.normalize();// Normalize.
dir.mult(13 / magn );
// dir.mult(0.5);// Scale.
acceleration = dir;// Set to acceleration.
//Motion 101! Velocity changes by acceleration. Location changes by velocity.
velocity.add(acceleration);
velocity.limit(topspeed);
location.add(velocity);
}
void display() {// Display the Mover
// stroke(0);
noStroke();
fill(250,255,100);
ellipse(location.x, location.y, 10, 10);
}
void checkEdges() {// What to do at the edges
if (location.x > width) {
location.x = 0;
} else if (location.x < 0) {
location.x = width;
}
if (location.y > height) {
location.y = 0;
} else if (location.y < 0) {
location.y = height;
}
}
}
リンク
素数のグラフィック http://www.datapointed.net/visualizations/math/factorization/animated-diagrams/?infinity