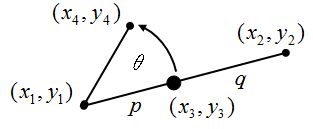生命情報アート論
(→ラングトンのアリ) |
(→共感覚) |
||
| (1人の利用者による、間の205版が非表示) | |||
| 3行: | 3行: | ||
*成績評価 | *成績評価 | ||
**出席:学生証scan+[http://www.kuhalabo.net/~web/examination/mpaper/min_paper.php?subj_id=3&grade=2 Minutes paper] | **出席:学生証scan+[http://www.kuhalabo.net/~web/examination/mpaper/min_paper.php?subj_id=3&grade=2 Minutes paper] | ||
| − | ** | + | **課題:セルオートマトン課題、再帰呼び出し図形課題、複素平面フラクタル課題 |
| − | **小テスト:[http://www. | + | **小テスト:[http://www.kuhalabo.net/~web/examination/result_highscore.php?subj_id=3 ハイスコア] |
| − | + | ||
;授業概要及び到達目標 | ;授業概要及び到達目標 | ||
| − | : | + | :インタラクティブアートは芸術を基盤として科学や工学を統合する新しい領域である。生物科学に関連した分野として、人工生命、ライフゲーム、フラクタル、オートマトン、遺伝的アルゴリズム、ニューラルネットワークなど応用範囲の広いものが数多く存在する。 |
| + | そういった生物に見られる特徴をアートに応用したジェネラティブアートの作品をC++のプログラミングを使用して、実際に作成してみる。 | ||
| + | |||
| + | 本講義の目標は以下の通り。 | ||
| + | |||
# 生物の特徴と生物的なシステムについて理解する。 | # 生物の特徴と生物的なシステムについて理解する。 | ||
# 複雑系システムについて理解し、応用例を作成できる。 | # 複雑系システムについて理解し、応用例を作成できる。 | ||
| − | # | + | # openFrameworksを使って作品のプログラミングができる。 |
| − | + | ||
| − | == | + | == アナウンス == |
| − | + | 開発環境として[[openFrameworks for Visual studio]]を使用します。 | |
| − | + | ||
| − | + | テキストや開発環境については、以下を参照してください。 | |
| − | + | * http://www.kuhalabo.net/kxoops/modules/d3blog/details.php?bid=141 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | 一年生の時にメディアプログラミング演習I程度のプログラミングスキルがあるものとして、授業を進めます。 | |
| − | + | もし、プログラミングに不安があるなら、上記テキストを使って、自分で予習や自習をしてください。 | |
| − | + | ||
| − | + | == 予定 == | |
| − | + | ;2014年度 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | # 9/30(火) ガイダンス, 生物と情報とアート,openFrameworksプログラミング演習 | |
| − | + | # 10/7(火) openFrameworks C++プログラミング | |
| − | + | # 10/14(火) 幾何学図形の描画 | |
| − | + | # 10/21(火) ランダムウォーク | |
| − | + | # 10/28(火) セルオートマトン | |
| − | + | # 11/4(火) セルオートマトン | |
| − | # 9/30( | + | # 11/11(火) セルオートマトン |
| − | + | # 11/18(火) セルオートマトン | |
| − | # 10/7( | + | # 11/25(火) セルオートマトン |
| − | # 10/14( | + | # 12/2(火) フラクタルと再帰呼び出し |
| − | # 10/ | + | # 12/9(火) 課題制作日 |
| − | # | + | # 12/16(火) フラクタルと再帰呼び出し |
| − | # 11/4( | + | # 1/6(火) 予備演習日(出席はとりません) |
| − | # 11/11( | + | # 1/20(火) 遺伝的アルゴリズム |
| − | # 11/18( | + | # 1/28(火) 小テスト |
| − | # 11/25( | + | |
| − | + | ||
| − | # 12/2( | + | |
| − | + | ||
| − | # 12/9( | + | |
| − | # 12/16( | + | |
| − | # 1/6( | + | |
| − | # 1/20( | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | # | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== 生物と情報とアート == | == 生物と情報とアート == | ||
| 215行: | 52行: | ||
* [http://www.kuhalabo.net/kxoops/modules/d3blog/details.php?bid=5 ヒト一人を再生するのに必要な情報量は?] | * [http://www.kuhalabo.net/kxoops/modules/d3blog/details.php?bid=5 ヒト一人を再生するのに必要な情報量は?] | ||
| − | + | == メモ == | |
| − | http:// | + | Visual Studioのショートカット |
| + | |||
| + | * Ctrl-K Ctrl-C コメントアウト | ||
| + | * Ctrl-K Ctrl-U コメントアウト解除 | ||
| + | * Ctrl-K Ctrl-F インデントをそろえる | ||
| + | |||
| + | [http://yoppa.org/ クリエイティブ・コーダー] | ||
== 複雑系 == | == 複雑系 == | ||
=== セルオートマトン === | === セルオートマトン === | ||
| − | *配布資料[http:// | + | *配布資料[http://www.kuhalabo.net/~kuha/tutorial0/bioart/cellautomaton2007.pdf PDF] |
*[http://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%A7%E3%83%AB%E3%83%94%E3%83%B3%E3%82%B9%E3%82%AD%E3%83%BC%E3%81%AE%E3%82%AE%E3%83%A3%E3%82%B9%E3%82%B1%E3%83%83%E3%83%88 シェルピンスキーのガスケット] | *[http://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%A7%E3%83%AB%E3%83%94%E3%83%B3%E3%82%B9%E3%82%AD%E3%83%BC%E3%81%AE%E3%82%AE%E3%83%A3%E3%82%B9%E3%82%B1%E3%83%83%E3%83%88 シェルピンスキーのガスケット] | ||
** [http://falconnet.peddie.org/students/2007/nburoojy/projects/cellular/ 256種類の1次元セルオートマトンの画像] / | ** [http://falconnet.peddie.org/students/2007/nburoojy/projects/cellular/ 256種類の1次元セルオートマトンの画像] / | ||
| 228行: | 71行: | ||
=== ライフゲーム === | === ライフゲーム === | ||
| − | [http:// | + | [http://www.kuhalabo.net/~kuha/tutorial0/bioart/Lifegame.exe ライフゲームの例] / |
[http://homepage3.nifty.com/izushi/LifeGame/ ライフゲーム入門] / | [http://homepage3.nifty.com/izushi/LifeGame/ ライフゲーム入門] / | ||
| − | [http:// | + | [http://www.kuhalabo.net/~kuha/tutorial0/bioart/cagallary/ セルオートマトン・ギャラリー] / |
;セルオートマトン音楽 | ;セルオートマトン音楽 | ||
| 236行: | 79行: | ||
[http://tamw.atari-users.net/camus.htm CAMUS]/ | [http://tamw.atari-users.net/camus.htm CAMUS]/ | ||
[http://www.glitchds.com/ Glitch DS]/ | [http://www.glitchds.com/ Glitch DS]/ | ||
| − | [http:// | + | [http://www.kuhalabo.net/lifegorch/ Life Game Orchestra] / |
;ギャラリー | ;ギャラリー | ||
| 250行: | 93行: | ||
[http://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%82%B0%E3%83%88%E3%83%B3%E3%81%AE%E3%82%A2%E3%83%AA ラングトンのアリ] / | [http://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%82%B0%E3%83%88%E3%83%B3%E3%81%AE%E3%82%A2%E3%83%AA ラングトンのアリ] / | ||
[http://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%82%B0%E3%83%88%E3%83%B3%E3%81%AE%E3%83%AB%E3%83%BC%E3%83%97 ラングトンのループ] / | [http://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%82%B0%E3%83%88%E3%83%B3%E3%81%AE%E3%83%AB%E3%83%BC%E3%83%97 ラングトンのループ] / | ||
| − | [http://necsi.org/postdocs/sayama/sdsr/java/ 自己増殖ループ] | + | [http://necsi.org/postdocs/sayama/sdsr/java/ 自己増殖ループ] / |
| + | [http://www.red3d.com/cwr/boids/ Reynolds Boid] / | ||
| − | + | http://www.local-guru.net/blog/2010/8/19/openframeworks-boid-demo | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | https://gist.github.com/tado/6603347 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Birds Algorhythm Craig Reynolds | ||
| + | http://processing.org/examples/flocking.html | ||
| − | == | + | == [[C Sharp Programming]] == |
| − | + | ||
| − | [ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== フラクタル == | == フラクタル == | ||
| 1,001行: | 112行: | ||
:古代エジプト人は3:4:5の辺を持つ三角形で直角が得られることを知っていた.ピラミッドなどの巨大建造物. | :古代エジプト人は3:4:5の辺を持つ三角形で直角が得られることを知っていた.ピラミッドなどの巨大建造物. | ||
:三平方の定理を発見したピタゴラスはどこがすごいか? | :三平方の定理を発見したピタゴラスはどこがすごいか? | ||
| − | |||
| − | |||
| − | |||
| − | |||
[http://www.gaia.h.kyoto-u.ac.jp/~fractal/ フラクタル日除け] | [http://www.gaia.h.kyoto-u.ac.jp/~fractal/ フラクタル日除け] | ||
== 自己相似系 == | == 自己相似系 == | ||
| − | + | === 再帰的呼出しによる樹木の描画 === | |
| − | + | *'''再帰的( recursive )呼び出し'''とは,サブルーチンや関数が,自分自身を呼び出すことをいう。樹木は,枝の1つを取り出して拡大しても,元の枝と同じ形(相似形)をしている。これは,同じサブルーチンで枝を描画しているからである。 | |
*再帰的呼出し的なCollaborate Flash Animation:[http://www.zoomquilt.org/ zoomquilt] ([http://www.media.t-kougei.ac.jp/~kuha/tutorial0/bioart/zoomquilt.swf swf]) | *再帰的呼出し的なCollaborate Flash Animation:[http://www.zoomquilt.org/ zoomquilt] ([http://www.media.t-kougei.ac.jp/~kuha/tutorial0/bioart/zoomquilt.swf swf]) | ||
| 1,176行: | 283行: | ||
Tane tane = new Tane(); | Tane tane = new Tane(); | ||
| − | |||
int n = 7; //子の世代数 | int n = 7; //子の世代数 | ||
double x0 = pictureBox1.Width * 0.1; //開始位置 x座標 | double x0 = pictureBox1.Width * 0.1; //開始位置 x座標 | ||
| 1,187行: | 293行: | ||
==== シダ葉の描画 ==== | ==== シダ葉の描画 ==== | ||
| + | ;ドラゴン図形の変化形 | ||
| + | * ドラゴン図形で使用した(x1,y1), (x2,y2), (x3,y3), (x4,y4), (x5,y5)を使う | ||
| + | * 直線(x1,y1)-(x2,y2), 直線(x1,y1)-(x4,y4), 直線(x3,y3)-(x5,y5)を基本図形とする。 | ||
[[ファイル:Sida2.JPG]] | [[ファイル:Sida2.JPG]] | ||
| 1,323行: | 432行: | ||
tane.Gene01(n, x0, y0, x1, y1, g, pen); | tane.Gene01(n, x0, y0, x1, y1, g, pen); | ||
</pre> | </pre> | ||
| + | |||
| + | ;マウスドラッグで始点と終点を決めて描く | ||
| + | *プロパティウィンドウにイベント(稲妻のアイコン)のリストを表示させ、MouseDownイベントをダブルクリックすると、MouseDownのメソッドが自動生成されます。 | ||
| + | *label1,label2に始点の座標を、label3, label4に終点の座標を入れる | ||
| + | |||
| + | <pre> | ||
| + | private void pictureBox1_MouseDown(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | label1.Text = e.X.ToString(); | ||
| + | label2.Text = e.Y.ToString(); | ||
| + | |||
| + | } | ||
| + | |||
| + | private void pictureBox1_MouseUp(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | Graphics g = pictureBox1.CreateGraphics(); | ||
| + | Pen pen = new Pen(Color.Green, 2); | ||
| + | Tane tane = new Tane(); | ||
| + | |||
| + | int n = 7; | ||
| + | double x0 = double.Parse(label1.Text); | ||
| + | double y0 = double.Parse(label2.Text); | ||
| + | double x1 = double.Parse(label3.Text); | ||
| + | double y1 = double.Parse(label4.Text); | ||
| + | |||
| + | tane.Gene01(n, x0, y0, x1, y1, g, pen); | ||
| + | } | ||
| + | |||
| + | private void pictureBox1_MouseMove(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | label3.Text = e.X.ToString(); | ||
| + | label4.Text = e.Y.ToString(); | ||
| + | |||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | p,q,thをクラスのメンバー変数にして、外部からランダムに与える。 | ||
| + | |||
| + | <pre> | ||
| + | class Tane | ||
| + | { | ||
| + | public double p { get; set; } | ||
| + | public double q { get; set; } | ||
| + | public double th { get; set; } | ||
| + | |||
| + | public void Gene01(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen) | ||
| + | { | ||
| + | double x3, y3, x4, y4; | ||
| + | double s = Math.Sin(th * Math.PI / 180.0); | ||
| + | double c = Math.Cos(th * Math.PI / 180.0); | ||
| + | |||
| + | if (n > 0) | ||
| + | { | ||
| + | x3 = (q * x1 + p * x2) / (p + q); | ||
| + | y3 = (q * y1 + p * y2) / (p + q); | ||
| + | x4 = x1 + (x3 - x1) * c - (y3 - y1) * s; | ||
| + | y4 = y1 + (x3 - x1) * s + (y3 - y1) * c; | ||
| + | pen.Color = Color.Yellow; | ||
| + | g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2); | ||
| + | g.DrawLine(pen, (float)x1, (float)y1, (float)x4, (float)y4); | ||
| + | Gene01(n - 1, x1, y1, x3, y3, g, pen); | ||
| + | Gene01(n - 1, x1, y1, x4, y4, g, pen); | ||
| + | Gene01(n - 1, x3, y3, x2, y2, g, pen); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | } | ||
| + | |||
| + | </pre> | ||
| + | |||
| + | <pre> | ||
| + | private void pictureBox1_MouseUp(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | Graphics g = pictureBox1.CreateGraphics(); | ||
| + | Pen pen = new Pen(Color.Green, 2); | ||
| + | Tane tane = new Tane(); | ||
| + | Random rnd = new Random(); | ||
| + | |||
| + | int n = 7; | ||
| + | double x0 = double.Parse(label1.Text); | ||
| + | double y0 = double.Parse(label2.Text); | ||
| + | double x1 = double.Parse(label3.Text); | ||
| + | double y1 = double.Parse(label4.Text); | ||
| + | |||
| + | tane.p = rnd.Next(2, 6); | ||
| + | tane.q = rnd.Next(3, 7); | ||
| + | tane.th = rnd.Next(10, 90); | ||
| + | |||
| + | tane.Gene01(n, x0, y0, x1, y1, g, pen); | ||
| + | } | ||
| + | |||
| + | </pre> | ||
| + | |||
| + | |||
==== タイマーを使用した樹木のアニメーション ==== | ==== タイマーを使用した樹木のアニメーション ==== | ||
| 1,362行: | 565行: | ||
== 複素平面フラクタル == | == 複素平面フラクタル == | ||
| − | *[http:// | + | *[http://blossom.media.t-kougei.ac.jp/~kuha/tutorial0/bioart/9_complex.pdf 配布資料PDF] |
| − | *[http:// | + | *[http://blossom.media.t-kougei.ac.jp/~kuha/tutorial0/bioart/mandelv3.exe 複複素平面フラクタル図形描画ソフトウェア for Windows] |
**注)comdlg32.ocxがない場合は,[http://www.microsoft.com/downloads/ja-jp/details.aspx?displaylang=ja&FamilyID=7B9BA261-7A9C-43E7-9117-F673077FFB3C ここ]からRuntimeファイル群をダウンロードしてください。 | **注)comdlg32.ocxがない場合は,[http://www.microsoft.com/downloads/ja-jp/details.aspx?displaylang=ja&FamilyID=7B9BA261-7A9C-43E7-9117-F673077FFB3C ここ]からRuntimeファイル群をダウンロードしてください。 | ||
| − | [http://www.youtube.com/watch?v= | + | [http://www.youtube.com/watch?v=0fKBhvDjuy0 Powers of Ten] |
| + | |||
| + | === C#の座標変換 === | ||
| + | ;座標原点 | ||
| + | 原点を移動するには、TranslateTransformメソッドを使う。 | ||
| + | <pre> | ||
| + | g.TranslateTransform(x1,y1); //座標原点を(x1,y1)に移動 | ||
| + | </pre> | ||
| + | |||
| + | ;座標の回転 | ||
| + | 座標軸をth度(degree)だけ回転するには、RotateTransformメソッドを使う。 | ||
| + | |||
| + | <pre> | ||
| + | g.RotateTransform(th); | ||
| + | </pre> | ||
| + | |||
| + | ;座標軸のスケール、方向 | ||
| + | 座標スケールを変換するには、ScaleTransformメソッドを使う。 | ||
| + | <pre> | ||
| + | g.ScaleTransform(scx,scy); //X軸をscx倍、Y軸をscy倍する | ||
| + | </pre> | ||
| + | X軸は右、Y軸は下が正方向なので、座標軸方向を反転するには、次のとおり。 | ||
| + | <pre> | ||
| + | g.ScaleTransform(1,-1); //Y軸方向の反転 | ||
| + | g.ScaleTransform(-1,1); //X軸方向の反転 | ||
| + | </pre> | ||
| + | |||
| + | === 複素平面フラクタルの描画 === | ||
| + | ;自己平方の描画プログラム | ||
| + | <pre> | ||
| + | Graphics g = pictureBox1.CreateGraphics(); | ||
| + | g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動 | ||
| + | g.ScaleTransform(1, -1); //Y軸の向きを反転 | ||
| + | Pen pen = new Pen(Color.White); | ||
| + | |||
| + | int Xmax = pictureBox1.Width / 2; | ||
| + | int Xmin = -pictureBox1.Width / 2; | ||
| + | int Ymax = pictureBox1.Height / 2; | ||
| + | int Ymin = -pictureBox1.Height / 2; | ||
| + | double Rmax = 0.5; | ||
| + | double Rmin = -0.5; | ||
| + | double Imax = 0.5; | ||
| + | double Imin = -0.5; | ||
| + | double Zr, newZr; | ||
| + | double Zi, newZi; | ||
| + | double Ar = -0.2; | ||
| + | double Ai = 0.675; | ||
| + | int Nmax = 100; | ||
| + | int Rstep = 1; // 何ピクセルごとに計算するか | ||
| + | int Istep = 1; | ||
| + | |||
| + | for (int x = Xmin; x < Xmax; x = x + Rstep) | ||
| + | { | ||
| + | for (int y = Ymin; y < Ymax; y = y + Istep) | ||
| + | { | ||
| + | Zr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Zの座標に変換 | ||
| + | Zi = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin; | ||
| + | int n = 0; | ||
| + | while ( Zr * Zr + Zi * Zi < 4 & n < Nmax ) | ||
| + | { | ||
| + | newZr = Zr * Zr - Zi * Zi + Ar; // f(z) = X^2 * Aの実数部 | ||
| + | newZi = 2 * Zr * Zi + Ai; // f(z) = X^2 * Aの虚数部 | ||
| + | Zr = newZr; | ||
| + | Zi = newZi; | ||
| + | n++; | ||
| + | } | ||
| + | if (n < Nmax) | ||
| + | { | ||
| + | pen.Color = Color.FromArgb(255, n * 255 / Nmax, 0, 0);//nの数に応じて色分ける | ||
| + | g.DrawRectangle(pen, x, y, 1, 1); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | ;マンデルブロー集合の描画プログラム | ||
| + | <pre> | ||
| + | Graphics g = pictureBox1.CreateGraphics(); | ||
| + | g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動 | ||
| + | g.ScaleTransform(1, -1); //Y軸の向きを反転 | ||
| + | Pen pen = new Pen(Color.White); | ||
| + | |||
| + | int Xmax = pictureBox1.Width / 2; | ||
| + | int Xmin = -pictureBox1.Width / 2; | ||
| + | int Ymax = pictureBox1.Height / 2; | ||
| + | int Ymin = -pictureBox1.Height / 2; | ||
| + | double Rmax = 1.5; | ||
| + | double Rmin = -1.5; | ||
| + | double Imax = 1.5; | ||
| + | double Imin = -1.5; | ||
| + | double Zr, newZr; | ||
| + | double Zi, newZi; | ||
| + | double Cr; | ||
| + | double Ci; | ||
| + | int Nmax = 50; | ||
| + | int Rstep = 1; // 何ピクセルごとに計算するか | ||
| + | int Istep = 1; | ||
| + | |||
| + | for (int x = Xmin; x < Xmax; x = x + Rstep) | ||
| + | { | ||
| + | for (int y = Ymin; y < Ymax; y = y + Istep) | ||
| + | { | ||
| + | Cr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Cの座標に変換 | ||
| + | Ci = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin; | ||
| + | int n = 0; | ||
| + | Zr = 0.0; | ||
| + | Zi = 0.0; | ||
| + | while (Zr * Zr + Zi * Zi < 4 & n < Nmax) | ||
| + | { | ||
| + | newZr = Zr * Zr - Zi * Zi + Cr; // f(z) = X^2 * Cの実数部 | ||
| + | newZi = 2 * Zr * Zi + Ci; // f(z) = X^2 * Cの虚数部 | ||
| + | Zr = newZr; | ||
| + | Zi = newZi; | ||
| + | n++; | ||
| + | } | ||
| + | if (n < Nmax) | ||
| + | { | ||
| + | pen.Color = Color.FromArgb(255, 0, n * 255 / Nmax, 0);//nの数に応じて色分ける | ||
| + | g.DrawRectangle(pen, x, y, 1, 1); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | ;Julia集合 | ||
| + | <pre> | ||
| + | Graphics g = pictureBox1.CreateGraphics(); | ||
| + | g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動 | ||
| + | g.ScaleTransform(1, -1); //Y軸の向きを反転 | ||
| + | Pen pen = new Pen(Color.White); | ||
| + | |||
| + | int Xmax = pictureBox1.Width / 2; | ||
| + | int Xmin = -pictureBox1.Width / 2; | ||
| + | int Ymax = pictureBox1.Height / 2; | ||
| + | int Ymin = -pictureBox1.Height / 2; | ||
| + | double Rmax = 1.5; | ||
| + | double Rmin = -1.5; | ||
| + | double Imax = 1.5; | ||
| + | double Imin = -1.5; | ||
| + | double Xr, Xr2, XrXi23, newXr; | ||
| + | double Xi, Xi2, newXi; | ||
| + | double Dr; | ||
| + | double Di; | ||
| + | int Nmax = 50; | ||
| + | int Rstep = 1; // 何ピクセルごとに計算するか | ||
| + | int Istep = 1; | ||
| + | |||
| + | for (int x = Xmin; x < Xmax; x = x + Rstep) | ||
| + | { | ||
| + | for (int y = Ymin; y < Ymax; y = y + Istep) | ||
| + | { | ||
| + | Xr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Cの座標に変換 | ||
| + | Xi = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin; | ||
| + | int n = 0; | ||
| + | Dr = 1.0; | ||
| + | Di = 1.0; | ||
| + | while (Dr + Di > 0.001 & n < Nmax) | ||
| + | { | ||
| + | Xr2 = Xr * Xr; | ||
| + | Xi2 = Xi * Xi; | ||
| + | XrXi23 = (Xr2 + Xi2) * (Xr2 + Xi2) / 3; | ||
| + | newXr = Xr * 2 / 3 + (Xr2 - Xi2) / XrXi23; // f(z) = X^2 * Cの実数部 | ||
| + | newXi = Xi * 2 / 3 - 2 * Xr * Xi / XrXi23; // f(z) = X^2 * Cの虚数部 | ||
| + | Dr = Math.Abs(newXr - Xr); | ||
| + | Di = Math.Abs(newXi - Xi); | ||
| + | Xr = newXr; | ||
| + | Xi = newXi; | ||
| + | n++; | ||
| + | } | ||
| + | if (n < Nmax) | ||
| + | { | ||
| + | int rr = n * 255 / Nmax; | ||
| + | int gg = 0; | ||
| + | int bb = 0; | ||
| + | pen.Color = Color.FromArgb(255, rr, gg, bb);//nの数に応じて色分ける | ||
| + | g.DrawRectangle(pen, x, y, 1, 1); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | === 配色の工夫 === | ||
| + | |||
| + | 個々の色の差をハッキリさせる。 | ||
| + | <pre> | ||
| + | int rr = (n % 13 + 1) * 255 / 14; | ||
| + | int gg = (n % 11 + 1) * 255 / 12; | ||
| + | int bb = (n % 7 + 1) * 255 / 8; | ||
| + | pen.Color = Color.FromArgb(255, rr, gg, bb); | ||
| + | g.DrawRectangle(pen, x, y, Rstep, Istep); | ||
| + | </pre> | ||
| + | |||
| + | ピクセルの目を粗くした時に、矩形の中身を塗りつぶす。 | ||
| + | <pre> | ||
| + | pen.Color = Color.FromArgb(255, rr, gg, bb); | ||
| + | brush.Color = Color.FromArgb(255, rr, gg, bb); | ||
| + | g.DrawRectangle(pen, x, y, Rstep, Istep); | ||
| + | g.FillRectangle(brush, x, y, Rstep, Istep); | ||
| + | </pre> | ||
| + | |||
| + | Ar, Ai, Rstep, Istepなどをテキストボックスから入力する。 | ||
| + | <pre> | ||
| + | Ar = double.Parse(textBox1.Text); | ||
| + | Ai = double.Parse(textBox2.Text); | ||
| + | |||
| + | Rstep = int.Parse(textBox3.Text); | ||
| + | Istep = Rstep; | ||
| + | </pre> | ||
| + | |||
| + | === いろいろカスタマイズ === | ||
| + | |||
| + | *複素平面の座標のスケールをラベルに表示する。 | ||
| + | *マウスドラッグで、新しく描画する範囲を選択する。 | ||
| + | *選択領域を正方形にするかどうかを、チェックボックスで指定する。 | ||
| + | <pre> | ||
| + | // グローバルに宣言 | ||
| + | Point MD = new Point();//マウスダウンの位置 | ||
| + | Point MU = new Point(); //マウスアップの位置 | ||
| + | |||
| + | bool view = false;//選択領域を描画するかどうかの判定 | ||
| + | bool view2 = false; | ||
| + | Graphics g; | ||
| + | int Xmax; | ||
| + | int Xmin; | ||
| + | int Ymax; | ||
| + | int Ymin; | ||
| + | |||
| + | double Rmax; | ||
| + | double Rmin; | ||
| + | double Imax; | ||
| + | double Imin; | ||
| + | |||
| + | double Rmax2;//マウスドラッグで指定した新しい範囲 | ||
| + | double Rmin2; | ||
| + | double Imax2; | ||
| + | double Imin2; | ||
| + | |||
| + | public Form1() | ||
| + | { | ||
| + | InitializeComponent(); | ||
| + | g = pictureBox1.CreateGraphics(); | ||
| + | g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動 | ||
| + | g.ScaleTransform(1, -1); //Y軸の向きを反転 | ||
| + | view2 = true; | ||
| + | |||
| + | Xmax = pictureBox1.Width / 2; | ||
| + | Xmin = -pictureBox1.Width / 2; | ||
| + | Ymax = pictureBox1.Height / 2; | ||
| + | Ymin = -pictureBox1.Height / 2; | ||
| + | |||
| + | Rmax2 = 0.5; | ||
| + | Rmin2 = -0.5; | ||
| + | Imax2 = 0.5; | ||
| + | Imin2 = -0.5; | ||
| + | Rmax = Rmax2; | ||
| + | Rmin = Rmin2; | ||
| + | Imax = Imax2; | ||
| + | Imin = Imin2; | ||
| + | |||
| + | label1.Text = null; | ||
| + | label2.Text = null; | ||
| + | label3.Text = null; | ||
| + | label4.Text = null; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | } | ||
| + | |||
| + | private void button1_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | Pen pen = new Pen(Color.White); | ||
| + | SolidBrush brush = new SolidBrush(Color.FromArgb(90, 200, 200, 200)); | ||
| + | |||
| + | g.Clear(Color.Black); //描画領域をクリア(黒で塗りつぶす) | ||
| + | |||
| + | Rmax = Rmax2; | ||
| + | Rmin = Rmin2; | ||
| + | Imax = Imax2; | ||
| + | Imin = Imin2; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | |||
| + | label5.Refresh(); | ||
| + | label6.Refresh(); | ||
| + | label7.Refresh(); | ||
| + | label8.Refresh(); | ||
| + | view2 = true; | ||
| + | |||
| + | double Zr, newZr; | ||
| + | double Zi, newZi; | ||
| + | double Ar = -0.2; | ||
| + | double Ai = 0.675; | ||
| + | // double Ar = -0.3; | ||
| + | // double Ai = 0.63; | ||
| + | Ar = double.Parse(textBox1.Text);//テキストボックスから値を取得 | ||
| + | Ai = double.Parse(textBox2.Text); | ||
| + | |||
| + | int Nmax = 500; | ||
| + | int Rstep = 3; // 何ピクセルごとに計算するか | ||
| + | int Istep = 3; | ||
| + | |||
| + | Rstep = int.Parse(textBox3.Text); | ||
| + | Istep = Rstep; | ||
| + | |||
| + | |||
| + | for (int x = Xmin; x < Xmax; x = x + Rstep) | ||
| + | { | ||
| + | for (int y = Ymin; y < Ymax; y = y + Istep) | ||
| + | { | ||
| + | Zr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Zの座標に変換 | ||
| + | Zi = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin; | ||
| + | int n = 0; | ||
| + | while ( Zr * Zr + Zi * Zi < 4 & n < Nmax ) | ||
| + | { | ||
| + | newZr = Zr * Zr - Zi * Zi + Ar; // f(z) = X^2 * Aの実数部 | ||
| + | newZi = 2 * Zr * Zi + Ai; // f(z) = X^2 * Aの虚数部 | ||
| + | Zr = newZr; | ||
| + | Zi = newZi; | ||
| + | n++; | ||
| + | } | ||
| + | if (n < Nmax) | ||
| + | { | ||
| + | int dr = 17; | ||
| + | int rr = (n % dr + 1) * 255 / (dr + 1); | ||
| + | int gg = (n % 11 + 1) * 255 / 12; | ||
| + | int bb = (n % 7 + 1) * 255 / 8; | ||
| + | pen.Color = Color.FromArgb(255, rr, gg, 255 - bb);//nの数に応じて色分ける | ||
| + | brush.Color = Color.FromArgb(255, rr, gg, 255 - bb);//nの数に応じて色分ける | ||
| + | g.DrawRectangle(pen, x, y, Rstep, Istep); | ||
| + | g.FillRectangle(brush, x, y, Rstep, Istep); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | private void button2_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | Graphics g = pictureBox1.CreateGraphics(); | ||
| + | g.Clear(Color.Black); //描画領域をクリア(黒で塗りつぶす) | ||
| + | |||
| + | label1.Text = null; | ||
| + | label2.Text = null; | ||
| + | label3.Text = null; | ||
| + | label4.Text = null; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | |||
| + | view2 = true; | ||
| + | |||
| + | } | ||
| + | |||
| + | // 以下、マウスイベントによって選択範囲を取得する処理 | ||
| + | private void pictureBox1_MouseDown(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | if (view2 == false) return; | ||
| + | // 描画フラグON | ||
| + | view = true; | ||
| + | |||
| + | // Mouseを押した座標を記録 | ||
| + | MD.X = e.X - Xmax; | ||
| + | MD.Y = Ymax - e.Y; | ||
| + | } | ||
| + | |||
| + | private void pictureBox1_MouseUp(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | if (view2 == false) return; | ||
| + | |||
| + | Point start = new Point(); | ||
| + | Point end = new Point(); | ||
| + | |||
| + | // Mouseを離した座標を記録 | ||
| + | MU.X = e.X - Xmax; | ||
| + | MU.Y = Ymax - e.Y; | ||
| + | |||
| + | // 座標から(X,Y)座標を計算 | ||
| + | GetRegion(MD, MU, ref start, ref end); | ||
| + | |||
| + | // 領域を描画 | ||
| + | DrawRegion(start, end); | ||
| + | |||
| + | // 描画フラグOFF | ||
| + | view = false; | ||
| + | view2 = false; | ||
| + | |||
| + | } | ||
| + | |||
| + | private void pictureBox1_MouseMove(object sender, MouseEventArgs e) | ||
| + | { | ||
| + | if (view2 == false) return; | ||
| + | |||
| + | Point p = new Point(); | ||
| + | |||
| + | p.X = e.X - Xmax; | ||
| + | p.Y = Ymax - e.Y; | ||
| + | |||
| + | // 描画フラグcheck | ||
| + | if (view == false) | ||
| + | { | ||
| + | label1.Text = ( ( p.X - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin ).ToString(); | ||
| + | label2.Text = ( ( p.Y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin ).ToString(); | ||
| + | |||
| + | label3.Text = null; | ||
| + | label4.Text = null; | ||
| + | |||
| + | return; | ||
| + | } | ||
| + | |||
| + | // カーソルが示している場所の座標を取得 | ||
| + | label3.Text = ( (p.X - Xmin) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin ).ToString(); | ||
| + | label4.Text = ( (p.Y - Ymin) * (Imax - Imin) / (Ymax - Ymin) + Imin ).ToString(); | ||
| + | } | ||
| + | |||
| + | private void GetRegion(Point p1, Point p2, ref Point start, ref Point end) | ||
| + | { | ||
| + | start.X = Math.Min(p1.X, p2.X); | ||
| + | start.Y = Math.Min(p1.Y, p2.Y); | ||
| + | |||
| + | end.X = Math.Max(p1.X, p2.X); | ||
| + | end.Y = Math.Max(p1.Y, p2.Y); | ||
| + | |||
| + | if (checkBox1.Checked == true) //選択領域を正方形にする | ||
| + | { | ||
| + | int min_x_y = Math.Min(Math.Abs(end.X - start.X), Math.Abs(end.Y - start.Y)); | ||
| + | |||
| + | end.X = start.X + min_x_y; | ||
| + | end.Y = start.Y + min_x_y; | ||
| + | } | ||
| + | |||
| + | Rmax2 = ( end.X - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Zの座標に変換 | ||
| + | Imax2 = ( end.Y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin; | ||
| + | Rmin2 = ( start.X - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; | ||
| + | Imin2 = ( start.Y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin; | ||
| + | } | ||
| + | |||
| + | private int GetLength(int start, int end) | ||
| + | { | ||
| + | return Math.Abs(start - end); | ||
| + | } | ||
| + | |||
| + | private void DrawRegion(Point start, Point end) | ||
| + | { | ||
| + | Pen blackPen = new Pen(Color.White); | ||
| + | SolidBrush tbrush = new SolidBrush(Color.FromArgb(100,220,220,220)); | ||
| + | |||
| + | // 描画する線を点線に設定 | ||
| + | // blackPen.DashStyle = System.Drawing.Drawing2D.DashStyle.Dash; | ||
| + | |||
| + | // 画面を消去 | ||
| + | // g.Clear(SystemColors.Control); | ||
| + | |||
| + | // 領域を描画 | ||
| + | g.DrawRectangle(blackPen, start.X, start.Y, GetLength(start.X, end.X), GetLength(start.Y, end.Y)); | ||
| + | g.FillRectangle(tbrush, start.X, start.Y, GetLength(start.X, end.X), GetLength(start.Y, end.Y)); | ||
| + | } | ||
| + | |||
| + | private void button5_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標を初期値に戻す | ||
| + | Rmax2 = 0.5; | ||
| + | Rmin2 = -0.5; | ||
| + | Imax2 = 0.5; | ||
| + | Imin2 = -0.5; | ||
| + | |||
| + | label1.Text = null; | ||
| + | label2.Text = null; | ||
| + | label3.Text = null; | ||
| + | label4.Text = null; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | *座標のスケールの拡大、縮小ボタンを付ける | ||
| + | <pre> | ||
| + | private void button6_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標のスケールを5倍にする | ||
| + | double ratio = 5.0; | ||
| + | double R_ave = ( Rmax2 + Rmin2 ) / 2; | ||
| + | double R_dif2 = ( Rmax2 - Rmin2 ) / 2; | ||
| + | double I_ave = ( Imax2 + Imin2 ) / 2; | ||
| + | double I_dif2 = ( Imax2 - Imin2 ) / 2; | ||
| + | |||
| + | Rmax2 = R_ave + R_dif2 * ratio; | ||
| + | Rmin2 = R_ave - R_dif2 * ratio; | ||
| + | Imax2 = I_ave + I_dif2 * ratio; | ||
| + | Imin2 = I_ave - I_dif2 * ratio; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | } | ||
| + | |||
| + | private void button7_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標のスケールを5分の1倍にする | ||
| + | double ratio = 5.0; | ||
| + | double R_ave = (Rmax2 + Rmin2) / 2; | ||
| + | double R_dif2 = (Rmax2 - Rmin2) / 2; | ||
| + | double I_ave = (Imax2 + Imin2) / 2; | ||
| + | double I_dif2 = (Imax2 - Imin2) / 2; | ||
| + | |||
| + | Rmax2 = R_ave + R_dif2 / ratio; | ||
| + | Rmin2 = R_ave - R_dif2 / ratio; | ||
| + | Imax2 = I_ave + I_dif2 / ratio; | ||
| + | Imin2 = I_ave - I_dif2 / ratio; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | |||
| + | *座標の上下左右へシフトさせるボタンを付ける | ||
| + | <pre> | ||
| + | private void button8_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標のスケールを左に0.5スケールシフトする | ||
| + | double R_ave = (Rmax2 + Rmin2) * 0.5; | ||
| + | double R_dif2 = (Rmax2 - Rmin2) * 0.5; | ||
| + | |||
| + | Rmax2 = Rmax2 - R_dif2; | ||
| + | Rmin2 = Rmin2 - R_dif2; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | } | ||
| + | |||
| + | private void button9_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標のスケールを右に0.5スケールシフトする | ||
| + | double R_ave = (Rmax2 + Rmin2) * 0.5; | ||
| + | double R_dif2 = (Rmax2 - Rmin2) * 0.5; | ||
| + | |||
| + | Rmax2 = Rmax2 + R_dif2; | ||
| + | Rmin2 = Rmin2 + R_dif2; | ||
| + | |||
| + | label5.Text = Rmax2.ToString(); | ||
| + | label6.Text = Rmin2.ToString(); | ||
| + | } | ||
| + | |||
| + | private void button10_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標のスケールを下に0.5スケールシフトする | ||
| + | double I_ave = (Imax2 + Imin2) * 0.5 ; | ||
| + | double I_dif2 = (Imax2 - Imin2) * 0.5; | ||
| + | |||
| + | Imax2 = Imax2 - I_dif2; | ||
| + | Imin2 = Imin2 - I_dif2; | ||
| + | |||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | } | ||
| + | |||
| + | private void button11_Click(object sender, EventArgs e) | ||
| + | { | ||
| + | // 座標のスケールを上に0.5スケールシフトする | ||
| + | double I_ave = (Imax2 + Imin2) * 0.5; | ||
| + | double I_dif2 = (Imax2 - Imin2) * 0.5; | ||
| + | |||
| + | Imax2 = Imax2 + I_dif2; | ||
| + | Imin2 = Imin2 + I_dif2; | ||
| + | |||
| + | label7.Text = Imax2.ToString(); | ||
| + | label8.Text = Imin2.ToString(); | ||
| + | } | ||
| + | </pre> | ||
== 人間の感覚 == | == 人間の感覚 == | ||
| 1,374行: | 1,157行: | ||
[http://w3.media.t-kougei.ac.jp/kuha/asp/asp00kuha/bbs.asp かんたん掲示板]に「香りの特徴」を書いてみよう。 | [http://w3.media.t-kougei.ac.jp/kuha/asp/asp00kuha/bbs.asp かんたん掲示板]に「香りの特徴」を書いてみよう。 | ||
| − | *[http://www. | + | *[http://www.kuhalabo.net/~kuha/doc/pclit_manu200510.pdf 香りの印刷] |
| − | *[http://www. | + | *[http://www.kuhalabo.net/~kuha/doc/aromap20040312.pdf アロマプリンタ] |
*[http://ja.wikipedia.org/wiki/RAMPO 映画RAMPO] | *[http://ja.wikipedia.org/wiki/RAMPO 映画RAMPO] | ||
*ブンマー・モンティエン,呼吸の家 | *ブンマー・モンティエン,呼吸の家 | ||
| 1,383行: | 1,166行: | ||
=== 共感覚 === | === 共感覚 === | ||
| − | *[http://www. | + | *[http://www.kuhalabo.net/~projectk/color_sound/trial-product/new/ 色彩と調性の関係性についての実験サイト](久原ゼミの実験企画) |
*[http://ist.ksc.kwansei.ac.jp/~nagata/synesthesia/ 色聴は共感覚](関西学院理工学部情報科学科の長田典子先生の研究室) | *[http://ist.ksc.kwansei.ac.jp/~nagata/synesthesia/ 色聴は共感覚](関西学院理工学部情報科学科の長田典子先生の研究室) | ||
| 1,417行: | 1,200行: | ||
[http://www.nhk.or.jp/digista/onair/hall_2004.html What is TRUTH?] / | [http://www.nhk.or.jp/digista/onair/hall_2004.html What is TRUTH?] / | ||
| − | *[http:// | + | *[http://blossom.media.t-kougei.ac.jp/~kuha/tutorial0/bioart/egg.swf Vector Parkのegg.swf] |
*[http://www.ebiebi.net//F_SAMPLES/clambon/ CLAMBON FARM] | *[http://www.ebiebi.net//F_SAMPLES/clambon/ CLAMBON FARM] | ||
*[http://intihuatani.usc.edu/cloud/flowing/ flOw] | *[http://intihuatani.usc.edu/cloud/flowing/ flOw] | ||
| − | *電子ペット Comたま [http:// | + | *電子ペット Comたま [http://blossom.media.t-kougei.ac.jp/comtama/ URL] / [http://blossom.media.t-kougei.ac.jp/~kuha/doc/genko_comtama.pdf PDF] |
| + | == [[脳]] == | ||
| − | == | + | == [[Neural Networks]] == |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | == [[Genetic Algorithm]] == | |
| − | + | == Github == | |
| + | 共同開発するときに便利。 | ||
| − | + | 学内のプロキシー環境で作業する場合、コンソールで | |
| + | <pre> | ||
| + | git config --global http.proxy proxy-n.t-kougei.ac.jp:8080 | ||
| + | git config --global https.proxy proxy-n.t-kougei.ac.jp:8080 | ||
| + | </pre> | ||
| + | とする。 | ||
| − | + | 通常のプロキシーのない環境で作業する場合、コンソールで | |
| + | <pre> | ||
| + | git config --global --unset http.proxy proxy-n.t-kougei.ac.jp:8080 | ||
| + | git config --global --unset https.proxy proxy-n.t-kougei.ac.jp:8080 | ||
| + | </pre> | ||
| + | とする。 | ||
| − | + | 現在の設定を確認するには、コンソールで、 | |
| − | + | <pre> | |
| − | + | git config --list | |
| − | + | </pre> | |
| − | + | とする。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== リンク == | == リンク == | ||
| 1,485行: | 1,238行: | ||
http://gushwell.ifdef.jp/ | http://gushwell.ifdef.jp/ | ||
| + | 素数のグラフィック | ||
| + | http://www.datapointed.net/visualizations/math/factorization/animated-diagrams/?infinity | ||
[[Category:授業]] | [[Category:授業]] | ||
2026年1月15日 (木) 10:16時点における最新版
目次 |
[編集] 概要
- 成績評価
- 出席:学生証scan+Minutes paper
- 課題:セルオートマトン課題、再帰呼び出し図形課題、複素平面フラクタル課題
- 小テスト:ハイスコア
- 授業概要及び到達目標
- インタラクティブアートは芸術を基盤として科学や工学を統合する新しい領域である。生物科学に関連した分野として、人工生命、ライフゲーム、フラクタル、オートマトン、遺伝的アルゴリズム、ニューラルネットワークなど応用範囲の広いものが数多く存在する。
そういった生物に見られる特徴をアートに応用したジェネラティブアートの作品をC++のプログラミングを使用して、実際に作成してみる。
本講義の目標は以下の通り。
- 生物の特徴と生物的なシステムについて理解する。
- 複雑系システムについて理解し、応用例を作成できる。
- openFrameworksを使って作品のプログラミングができる。
[編集] アナウンス
開発環境としてopenFrameworks for Visual studioを使用します。
テキストや開発環境については、以下を参照してください。
一年生の時にメディアプログラミング演習I程度のプログラミングスキルがあるものとして、授業を進めます。 もし、プログラミングに不安があるなら、上記テキストを使って、自分で予習や自習をしてください。
[編集] 予定
- 2014年度
- 9/30(火) ガイダンス, 生物と情報とアート,openFrameworksプログラミング演習
- 10/7(火) openFrameworks C++プログラミング
- 10/14(火) 幾何学図形の描画
- 10/21(火) ランダムウォーク
- 10/28(火) セルオートマトン
- 11/4(火) セルオートマトン
- 11/11(火) セルオートマトン
- 11/18(火) セルオートマトン
- 11/25(火) セルオートマトン
- 12/2(火) フラクタルと再帰呼び出し
- 12/9(火) 課題制作日
- 12/16(火) フラクタルと再帰呼び出し
- 1/6(火) 予備演習日(出席はとりません)
- 1/20(火) 遺伝的アルゴリズム
- 1/28(火) 小テスト
[編集] 生物と情報とアート
- 生物とは? 生物の特徴とは?
- 例:小石と貝殻
- * 簡単BBSに「生物と無生物の違いは何か?」説明してみよう。
- ゲノムのDNAマップ NCBI Map Viewer
- ヒト一人を再生するのに必要な情報量は?
[編集] メモ
Visual Studioのショートカット
- Ctrl-K Ctrl-C コメントアウト
- Ctrl-K Ctrl-U コメントアウト解除
- Ctrl-K Ctrl-F インデントをそろえる
[編集] 複雑系
[編集] セルオートマトン
[編集] ライフゲーム
ライフゲームの例 / ライフゲーム入門 / セルオートマトン・ギャラリー /
- セルオートマトン音楽
WolframTones/ CAMUS/ Glitch DS/ Life Game Orchestra /
- ギャラリー
Modern Cellular Automata/ CArt gallery/ Cellular Automata Art/ ASCII Art Cell Automaton/
- 参考
ワイヤワールド /
[編集] 人工生命
ラングトンのアリ / ラングトンのループ / 自己増殖ループ / Reynolds Boid /
http://www.local-guru.net/blog/2010/8/19/openframeworks-boid-demo
https://gist.github.com/tado/6603347
Birds Algorhythm Craig Reynolds
http://processing.org/examples/flocking.html
[編集] C Sharp Programming
[編集] フラクタル
古代ギリシャからあるユークリッド幾何学と20世紀のフラクタル幾何学の比較
- 考察
- 古代エジプト人は3:4:5の辺を持つ三角形で直角が得られることを知っていた.ピラミッドなどの巨大建造物.
- 三平方の定理を発見したピタゴラスはどこがすごいか?
[編集] 自己相似系
[編集] 再帰的呼出しによる樹木の描画
- 再帰的( recursive )呼び出しとは,サブルーチンや関数が,自分自身を呼び出すことをいう。樹木は,枝の1つを取り出して拡大しても,元の枝と同じ形(相似形)をしている。これは,同じサブルーチンで枝を描画しているからである。
[編集] C#による実装
[編集] 新しいクラスの定義
- 「プロジェクト」メニューから「クラスの追加」で新しいクラス名を入力する。クラスの定義の中にメソッドを記述する。
- 注意
using System.Drawing;
をTane.csの冒頭に追加
[編集] 樹木の描画
- Taneクラスのメソッド
線分(x1,y1)-(x2,y2)が与えられたら、(x2,y2)の先端に(x3,y3), (x4,y4)を取り、線分(x2,y2)-(x3,y3)と線分(x2,y2)-(x4,y4)を描画する。
class Tane
{
public void Eda(int n, double x1, double y1, double x2, double y2, double angle, Graphics g, Pen pen)
{
double x3, y3, x4, y4;
double s = Math.Sin(angle * Math.PI / 180.0);
double c = Math.Cos(angle * Math.PI / 180.0);
double dx = 0.7 * (x2 - x1);
double dy = 0.7 * (y2 - y1);
if (n > 0)
{
x3 = x2 + dx * c - dy * s;
y3 = y2 + dx * s + dy * c;
x4 = x2 + dx * c + dy * s;
y4 = y2 - dx * s + dy * c;
// 枝を描画する
g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
g.DrawLine(pen, (float)x2, (float)y2, (float)x3, (float)y3);
g.DrawLine(pen, (float)x2, (float)y2, (float)x4, (float)y4);
//子の再起呼び出し
Eda(n - 1, x2, y2, x3, y3, angle, g, pen);
Eda(n - 1, x2, y2, x4, y4, angle, g, pen);
}
}
}
- 樹木描画ボタンクリックの中身
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
int n = 10; //枝の世代数
double x0 = pictureBox1.Width / 2; //開始位置 x座標
double y0 = pictureBox1.Height; //開始位置 y座標
double x1 = pictureBox1.Width / 2; //開始位置 x座標
double y1 = pictureBox1.Height * 0.8; //開始位置 y座標
double angle = 30.0; //子供の枝の角度の差分
tane.Eda(n, x0, y0, x1, y1, angle, g, pen);
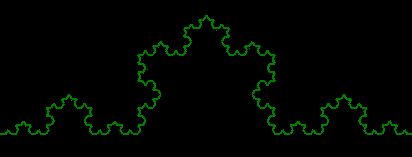
[編集] コッホ図形の描画
- Taneクラスのメソッド
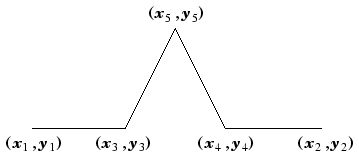
public void Koch(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
{
double x3, y3, x4, y4, x5, y5;
double s = Math.Sin(Math.PI / 3.0);
double c = Math.Cos(Math.PI / 3.0);
if (n > 0)
{
x3 = (2 * x1 + x2) / 3.0;
y3 = (2 * y1 + y2) / 3.0;
x4 = (x1 + 2 * x2) / 3.0;
y4 = (y1 + 2 * y2) / 3.0;
x5 = x3 + (x4 - x3) * c + (y4 - y3) * s;
y5 = y3 - (x4 - x3) * s + (y4 - y3) * c;
// ジェネレータを描画する
pen.Color = Color.Black;
g.DrawLine(pen, (float)x3, (float)y3, (float)x4, (float)y4);
pen.Color = Color.Green;
g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
g.DrawLine(pen, (float)x3, (float)y3, (float)x5, (float)y5);
g.DrawLine(pen, (float)x5, (float)y5, (float)x4, (float)y4);
g.DrawLine(pen, (float)x4, (float)y4, (float)x2, (float)y2);
// 子の再起呼び出し
Koch(n - 1, x1, y1, x3, y3, g, pen);
Koch(n - 1, x3, y3, x5, y5, g, pen);
Koch(n - 1, x5, y5, x4, y4, g, pen);
Koch(n - 1, x4, y4, x2, y2, g, pen);
}
}
- コッホ図形描画ボタンクリックの中身
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
// マウス位置へ直線を描画する
int n = 4; //子の世代数
double x0 = 0; //開始位置 x座標
double y0 = pictureBox1.Height * 0.6 ; //開始位置 y座標
double x1 = pictureBox1.Width; //終了位置 x座標
double y1 = pictureBox1.Height * 0.6; //終了位置 y座標
tane.Koch(n, x0, y0, x1, y1, g, pen);
[編集] ドラゴン図形の描画
- Taneクラスのメソッド
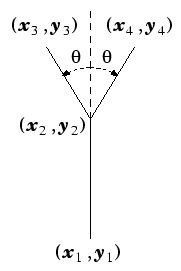
public void Dragon(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
{
double x3, y3, x4, y4, x5, y5;
if (n > 0)
{
x3 = 0.5 * ( x1 + x2);
y3 = 0.5 * ( y1 + y2);
x4 = 0.5 * (x1 + x3 - y1 + y3);
y4 = 0.5 * (x1 - x3 + y1 + y3);
x5 = 0.5 * (x2 + x3 - y2 + y3);
y5 = 0.5 * (x2 - x3 + y2 + y3);
// 枝を描画する
pen.Color = Color.Black;
g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
g.DrawLine(pen, (float)x3, (float)y3, (float)x2, (float)y2);
pen.Color = Color.Green;
g.DrawLine(pen, (float)x1, (float)y1, (float)x4, (float)y4);
g.DrawLine(pen, (float)x4, (float)y4, (float)x3, (float)y3);
g.DrawLine(pen, (float)x3, (float)y3, (float)x5, (float)y5);
g.DrawLine(pen, (float)x5, (float)y5, (float)x2, (float)y2);
Dragon(n - 1, x1, y1, x4, y4, g, pen);
Dragon(n - 1, x4, y4, x3, y3, g, pen);
Dragon(n - 1, x3, y3, x5, y5, g, pen);
Dragon(n - 1, x5, y5, x2, y2, g, pen);
}
}
- ドラゴン図形描画ボタンクリックの中身
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
int n = 7; //子の世代数
double x0 = pictureBox1.Width * 0.1; //開始位置 x座標
double y0 = pictureBox1.Height * 0.5; //開始位置 y座標
double x1 = pictureBox1.Width * 0.9; //終了位置 x座標
double y1 = pictureBox1.Height * 0.5; //終了位置 y座標
tane.Dragon(n, x0, y0, x1, y1, g, pen);
[編集] シダ葉の描画
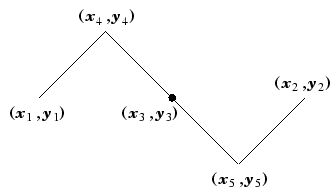
- ドラゴン図形の変化形
- ドラゴン図形で使用した(x1,y1), (x2,y2), (x3,y3), (x4,y4), (x5,y5)を使う
- 直線(x1,y1)-(x2,y2), 直線(x1,y1)-(x4,y4), 直線(x3,y3)-(x5,y5)を基本図形とする。
- Taneクラスのメソッド
public void Fern(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
{
double x3, y3, x4, y4, x5, y5;
if (n > 0)
{
x3 = ( x1 + x2 ) / 2.0;
y3 = ( y1 + y2 ) / 2.0;
x4 = ( x1 + x3 - y1 + y3) / 2.0;
y4 = ( x1 - x3 + y1 + y3) / 2.0;
x5 = ( x2 + x3 - y2 + y3) / 2.0;
y5 = ( x2 - x3 + y2 + y3) / 2.0;
// 枝を描画する
pen.Color = Color.Green;
g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
g.DrawLine(pen, (float)x3, (float)y3, (float)x5, (float)y5);
Fern(n - 1, x1, y1, x4, y4, g, pen);
Fern(n - 1, x1, y1, x3, y3, g, pen);
Fern(n - 1, x3, y3, x2, y2, g, pen);
Fern(n - 1, x3, y3, x5, y5, g, pen);
}
}
- シダ葉描画ボタンクリックの中身
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
int n = 7; //子の世代数
double x0 = pictureBox1.Width * 0.1; //開始位置 x座標
double y0 = pictureBox1.Height * 0.5; //開始位置 y座標
double x1 = pictureBox1.Width * 0.9; //終了位置 x座標
double y1 = pictureBox1.Height * 0.5; //終了位置 y座標
tane.Fern(n, x0, y0, x1, y1, g, pen);
[編集] Cカーブの描画
- Taneクラスのメソッド
public void Ccurve(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
{
double x3, y3;
if (n > 0)
{
x3 = 0.5 * (x1 + x2 - y1 + y2);
y3 = 0.5 * (x1 - x2 + y1 + y2);
// 枝を描画する
pen.Color = Color.Black;
g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
pen.Color = Color.Green;
g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
g.DrawLine(pen, (float)x3, (float)y3, (float)x2, (float)y2);
Ccurve(n - 1, x1, y1, x3, y3, g, pen);
Ccurve(n - 1, x3, y3, x2, y2, g, pen);
}
}
- Cカーブ画ボタンクリックの中身
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
int n = 12; //子の世代数
double x0 = pictureBox1.Width * 0.25; //開始位置 x座標
double y0 = pictureBox1.Height * 0.75; //開始位置 y座標
double x1 = pictureBox1.Width * 0.75; //終了位置 x座標
double y1 = pictureBox1.Height * 0.75; //終了位置 y座標
tane.Ccurve(n, x0, y0, x1, y1, g, pen);
[編集] 内分点と回転によるカスタムジェネレータの描画
- Taneクラスのメソッド
public void Gene01(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
{
double x3, y3, x4, y4;
double p = 2.0;
double q = 3.0;
double th = -30.0;
double s = Math.Sin(th * Math.PI / 180.0);
double c = Math.Cos(th * Math.PI / 180.0);
if (n > 0)
{
x3 = (q * x1 + p * x2) / (p + q);
y3 = (q * y1 + p * y2) / (p + q);
x4 = x1 + (x3 - x1) * c - (y3 - y1) * s;
y4 = y1 + (x3 - x1) * s + (y3 - y1) * c;
pen.Color = Color.Yellow;
g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
g.DrawLine(pen, (float)x1, (float)y1, (float)x4, (float)y4);
Gene01(n - 1, x1, y1, x3, y3, g, pen);
Gene01(n - 1, x1, y1, x4, y4, g, pen);
Gene01(n - 1, x3, y3, x2, y2, g, pen);
}
}
- カスタムジェネレータ描画ボタンクリックの中身
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
int n = 7; //子の世代数
double x0 = pictureBox1.Width * 0.1; //開始位置 x座標
double y0 = pictureBox1.Height * 0.5; //開始位置 y座標
double x1 = pictureBox1.Width * 0.9; //終了位置 x座標
double y1 = pictureBox1.Height * 0.5; //終了位置 y座標
tane.Gene01(n, x0, y0, x1, y1, g, pen);
- マウスドラッグで始点と終点を決めて描く
- プロパティウィンドウにイベント(稲妻のアイコン)のリストを表示させ、MouseDownイベントをダブルクリックすると、MouseDownのメソッドが自動生成されます。
- label1,label2に始点の座標を、label3, label4に終点の座標を入れる
private void pictureBox1_MouseDown(object sender, MouseEventArgs e)
{
label1.Text = e.X.ToString();
label2.Text = e.Y.ToString();
}
private void pictureBox1_MouseUp(object sender, MouseEventArgs e)
{
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
int n = 7;
double x0 = double.Parse(label1.Text);
double y0 = double.Parse(label2.Text);
double x1 = double.Parse(label3.Text);
double y1 = double.Parse(label4.Text);
tane.Gene01(n, x0, y0, x1, y1, g, pen);
}
private void pictureBox1_MouseMove(object sender, MouseEventArgs e)
{
label3.Text = e.X.ToString();
label4.Text = e.Y.ToString();
}
p,q,thをクラスのメンバー変数にして、外部からランダムに与える。
class Tane
{
public double p { get; set; }
public double q { get; set; }
public double th { get; set; }
public void Gene01(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
{
double x3, y3, x4, y4;
double s = Math.Sin(th * Math.PI / 180.0);
double c = Math.Cos(th * Math.PI / 180.0);
if (n > 0)
{
x3 = (q * x1 + p * x2) / (p + q);
y3 = (q * y1 + p * y2) / (p + q);
x4 = x1 + (x3 - x1) * c - (y3 - y1) * s;
y4 = y1 + (x3 - x1) * s + (y3 - y1) * c;
pen.Color = Color.Yellow;
g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
g.DrawLine(pen, (float)x1, (float)y1, (float)x4, (float)y4);
Gene01(n - 1, x1, y1, x3, y3, g, pen);
Gene01(n - 1, x1, y1, x4, y4, g, pen);
Gene01(n - 1, x3, y3, x2, y2, g, pen);
}
}
}
private void pictureBox1_MouseUp(object sender, MouseEventArgs e)
{
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 2);
Tane tane = new Tane();
Random rnd = new Random();
int n = 7;
double x0 = double.Parse(label1.Text);
double y0 = double.Parse(label2.Text);
double x1 = double.Parse(label3.Text);
double y1 = double.Parse(label4.Text);
tane.p = rnd.Next(2, 6);
tane.q = rnd.Next(3, 7);
tane.th = rnd.Next(10, 90);
tane.Gene01(n, x0, y0, x1, y1, g, pen);
}
[編集] タイマーを使用した樹木のアニメーション
private void button3_Click(object sender, EventArgs e)
{
timer1.Enabled = true;
timer1.Start();
}
private void button4_Click(object sender, EventArgs e)
{
timer1.Stop();
timer1.Enabled = false;
}
public int cnt; //タイマー用カウンタ
private void timer1_Tick(object sender, EventArgs e)
{
Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Green, 1);
Tane tane = new Tane();
g.Clear(Color.Black);
cnt++; //タイマー用カウンタのカウントアップ
int n = 10; //枝の世代数
double x0 = pictureBox1.Width / 2; //開始位置 x座標
double y0 = pictureBox1.Height; //開始位置 y座標
double x1 = pictureBox1.Width / 2; //開始位置 x座標
double y1 = pictureBox1.Height * 0.9 - cnt * 2; //開始位置 y座標
double angle = 30.0; //子供の枝の角度の変化の差分
double a_rate = angle + cnt * 2;
tane.Eda(n, x0, y0, x1, y1, a_rate, g, pen);
}
[編集] 複素平面フラクタル
- 配布資料PDF
- 複複素平面フラクタル図形描画ソフトウェア for Windows
- 注)comdlg32.ocxがない場合は,ここからRuntimeファイル群をダウンロードしてください。
[編集] C#の座標変換
- 座標原点
原点を移動するには、TranslateTransformメソッドを使う。
g.TranslateTransform(x1,y1); //座標原点を(x1,y1)に移動
- 座標の回転
座標軸をth度(degree)だけ回転するには、RotateTransformメソッドを使う。
g.RotateTransform(th);
- 座標軸のスケール、方向
座標スケールを変換するには、ScaleTransformメソッドを使う。
g.ScaleTransform(scx,scy); //X軸をscx倍、Y軸をscy倍する
X軸は右、Y軸は下が正方向なので、座標軸方向を反転するには、次のとおり。
g.ScaleTransform(1,-1); //Y軸方向の反転 g.ScaleTransform(-1,1); //X軸方向の反転
[編集] 複素平面フラクタルの描画
- 自己平方の描画プログラム
Graphics g = pictureBox1.CreateGraphics();
g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動
g.ScaleTransform(1, -1); //Y軸の向きを反転
Pen pen = new Pen(Color.White);
int Xmax = pictureBox1.Width / 2;
int Xmin = -pictureBox1.Width / 2;
int Ymax = pictureBox1.Height / 2;
int Ymin = -pictureBox1.Height / 2;
double Rmax = 0.5;
double Rmin = -0.5;
double Imax = 0.5;
double Imin = -0.5;
double Zr, newZr;
double Zi, newZi;
double Ar = -0.2;
double Ai = 0.675;
int Nmax = 100;
int Rstep = 1; // 何ピクセルごとに計算するか
int Istep = 1;
for (int x = Xmin; x < Xmax; x = x + Rstep)
{
for (int y = Ymin; y < Ymax; y = y + Istep)
{
Zr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Zの座標に変換
Zi = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin;
int n = 0;
while ( Zr * Zr + Zi * Zi < 4 & n < Nmax )
{
newZr = Zr * Zr - Zi * Zi + Ar; // f(z) = X^2 * Aの実数部
newZi = 2 * Zr * Zi + Ai; // f(z) = X^2 * Aの虚数部
Zr = newZr;
Zi = newZi;
n++;
}
if (n < Nmax)
{
pen.Color = Color.FromArgb(255, n * 255 / Nmax, 0, 0);//nの数に応じて色分ける
g.DrawRectangle(pen, x, y, 1, 1);
}
}
}
- マンデルブロー集合の描画プログラム
Graphics g = pictureBox1.CreateGraphics();
g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動
g.ScaleTransform(1, -1); //Y軸の向きを反転
Pen pen = new Pen(Color.White);
int Xmax = pictureBox1.Width / 2;
int Xmin = -pictureBox1.Width / 2;
int Ymax = pictureBox1.Height / 2;
int Ymin = -pictureBox1.Height / 2;
double Rmax = 1.5;
double Rmin = -1.5;
double Imax = 1.5;
double Imin = -1.5;
double Zr, newZr;
double Zi, newZi;
double Cr;
double Ci;
int Nmax = 50;
int Rstep = 1; // 何ピクセルごとに計算するか
int Istep = 1;
for (int x = Xmin; x < Xmax; x = x + Rstep)
{
for (int y = Ymin; y < Ymax; y = y + Istep)
{
Cr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Cの座標に変換
Ci = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin;
int n = 0;
Zr = 0.0;
Zi = 0.0;
while (Zr * Zr + Zi * Zi < 4 & n < Nmax)
{
newZr = Zr * Zr - Zi * Zi + Cr; // f(z) = X^2 * Cの実数部
newZi = 2 * Zr * Zi + Ci; // f(z) = X^2 * Cの虚数部
Zr = newZr;
Zi = newZi;
n++;
}
if (n < Nmax)
{
pen.Color = Color.FromArgb(255, 0, n * 255 / Nmax, 0);//nの数に応じて色分ける
g.DrawRectangle(pen, x, y, 1, 1);
}
}
}
- Julia集合
Graphics g = pictureBox1.CreateGraphics();
g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動
g.ScaleTransform(1, -1); //Y軸の向きを反転
Pen pen = new Pen(Color.White);
int Xmax = pictureBox1.Width / 2;
int Xmin = -pictureBox1.Width / 2;
int Ymax = pictureBox1.Height / 2;
int Ymin = -pictureBox1.Height / 2;
double Rmax = 1.5;
double Rmin = -1.5;
double Imax = 1.5;
double Imin = -1.5;
double Xr, Xr2, XrXi23, newXr;
double Xi, Xi2, newXi;
double Dr;
double Di;
int Nmax = 50;
int Rstep = 1; // 何ピクセルごとに計算するか
int Istep = 1;
for (int x = Xmin; x < Xmax; x = x + Rstep)
{
for (int y = Ymin; y < Ymax; y = y + Istep)
{
Xr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Cの座標に変換
Xi = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin;
int n = 0;
Dr = 1.0;
Di = 1.0;
while (Dr + Di > 0.001 & n < Nmax)
{
Xr2 = Xr * Xr;
Xi2 = Xi * Xi;
XrXi23 = (Xr2 + Xi2) * (Xr2 + Xi2) / 3;
newXr = Xr * 2 / 3 + (Xr2 - Xi2) / XrXi23; // f(z) = X^2 * Cの実数部
newXi = Xi * 2 / 3 - 2 * Xr * Xi / XrXi23; // f(z) = X^2 * Cの虚数部
Dr = Math.Abs(newXr - Xr);
Di = Math.Abs(newXi - Xi);
Xr = newXr;
Xi = newXi;
n++;
}
if (n < Nmax)
{
int rr = n * 255 / Nmax;
int gg = 0;
int bb = 0;
pen.Color = Color.FromArgb(255, rr, gg, bb);//nの数に応じて色分ける
g.DrawRectangle(pen, x, y, 1, 1);
}
}
}
[編集] 配色の工夫
個々の色の差をハッキリさせる。
int rr = (n % 13 + 1) * 255 / 14;
int gg = (n % 11 + 1) * 255 / 12;
int bb = (n % 7 + 1) * 255 / 8;
pen.Color = Color.FromArgb(255, rr, gg, bb);
g.DrawRectangle(pen, x, y, Rstep, Istep);
ピクセルの目を粗くした時に、矩形の中身を塗りつぶす。
pen.Color = Color.FromArgb(255, rr, gg, bb);
brush.Color = Color.FromArgb(255, rr, gg, bb);
g.DrawRectangle(pen, x, y, Rstep, Istep);
g.FillRectangle(brush, x, y, Rstep, Istep);
Ar, Ai, Rstep, Istepなどをテキストボックスから入力する。
Ar = double.Parse(textBox1.Text);
Ai = double.Parse(textBox2.Text);
Rstep = int.Parse(textBox3.Text);
Istep = Rstep;
[編集] いろいろカスタマイズ
- 複素平面の座標のスケールをラベルに表示する。
- マウスドラッグで、新しく描画する範囲を選択する。
- 選択領域を正方形にするかどうかを、チェックボックスで指定する。
// グローバルに宣言
Point MD = new Point();//マウスダウンの位置
Point MU = new Point(); //マウスアップの位置
bool view = false;//選択領域を描画するかどうかの判定
bool view2 = false;
Graphics g;
int Xmax;
int Xmin;
int Ymax;
int Ymin;
double Rmax;
double Rmin;
double Imax;
double Imin;
double Rmax2;//マウスドラッグで指定した新しい範囲
double Rmin2;
double Imax2;
double Imin2;
public Form1()
{
InitializeComponent();
g = pictureBox1.CreateGraphics();
g.TranslateTransform(pictureBox1.Width / 2, pictureBox1.Height / 2); //原点を中央に移動
g.ScaleTransform(1, -1); //Y軸の向きを反転
view2 = true;
Xmax = pictureBox1.Width / 2;
Xmin = -pictureBox1.Width / 2;
Ymax = pictureBox1.Height / 2;
Ymin = -pictureBox1.Height / 2;
Rmax2 = 0.5;
Rmin2 = -0.5;
Imax2 = 0.5;
Imin2 = -0.5;
Rmax = Rmax2;
Rmin = Rmin2;
Imax = Imax2;
Imin = Imin2;
label1.Text = null;
label2.Text = null;
label3.Text = null;
label4.Text = null;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
}
private void button1_Click(object sender, EventArgs e)
{
Pen pen = new Pen(Color.White);
SolidBrush brush = new SolidBrush(Color.FromArgb(90, 200, 200, 200));
g.Clear(Color.Black); //描画領域をクリア(黒で塗りつぶす)
Rmax = Rmax2;
Rmin = Rmin2;
Imax = Imax2;
Imin = Imin2;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
label5.Refresh();
label6.Refresh();
label7.Refresh();
label8.Refresh();
view2 = true;
double Zr, newZr;
double Zi, newZi;
double Ar = -0.2;
double Ai = 0.675;
// double Ar = -0.3;
// double Ai = 0.63;
Ar = double.Parse(textBox1.Text);//テキストボックスから値を取得
Ai = double.Parse(textBox2.Text);
int Nmax = 500;
int Rstep = 3; // 何ピクセルごとに計算するか
int Istep = 3;
Rstep = int.Parse(textBox3.Text);
Istep = Rstep;
for (int x = Xmin; x < Xmax; x = x + Rstep)
{
for (int y = Ymin; y < Ymax; y = y + Istep)
{
Zr = ( x - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Zの座標に変換
Zi = ( y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin;
int n = 0;
while ( Zr * Zr + Zi * Zi < 4 & n < Nmax )
{
newZr = Zr * Zr - Zi * Zi + Ar; // f(z) = X^2 * Aの実数部
newZi = 2 * Zr * Zi + Ai; // f(z) = X^2 * Aの虚数部
Zr = newZr;
Zi = newZi;
n++;
}
if (n < Nmax)
{
int dr = 17;
int rr = (n % dr + 1) * 255 / (dr + 1);
int gg = (n % 11 + 1) * 255 / 12;
int bb = (n % 7 + 1) * 255 / 8;
pen.Color = Color.FromArgb(255, rr, gg, 255 - bb);//nの数に応じて色分ける
brush.Color = Color.FromArgb(255, rr, gg, 255 - bb);//nの数に応じて色分ける
g.DrawRectangle(pen, x, y, Rstep, Istep);
g.FillRectangle(brush, x, y, Rstep, Istep);
}
}
}
}
private void button2_Click(object sender, EventArgs e)
{
Graphics g = pictureBox1.CreateGraphics();
g.Clear(Color.Black); //描画領域をクリア(黒で塗りつぶす)
label1.Text = null;
label2.Text = null;
label3.Text = null;
label4.Text = null;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
view2 = true;
}
// 以下、マウスイベントによって選択範囲を取得する処理
private void pictureBox1_MouseDown(object sender, MouseEventArgs e)
{
if (view2 == false) return;
// 描画フラグON
view = true;
// Mouseを押した座標を記録
MD.X = e.X - Xmax;
MD.Y = Ymax - e.Y;
}
private void pictureBox1_MouseUp(object sender, MouseEventArgs e)
{
if (view2 == false) return;
Point start = new Point();
Point end = new Point();
// Mouseを離した座標を記録
MU.X = e.X - Xmax;
MU.Y = Ymax - e.Y;
// 座標から(X,Y)座標を計算
GetRegion(MD, MU, ref start, ref end);
// 領域を描画
DrawRegion(start, end);
// 描画フラグOFF
view = false;
view2 = false;
}
private void pictureBox1_MouseMove(object sender, MouseEventArgs e)
{
if (view2 == false) return;
Point p = new Point();
p.X = e.X - Xmax;
p.Y = Ymax - e.Y;
// 描画フラグcheck
if (view == false)
{
label1.Text = ( ( p.X - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin ).ToString();
label2.Text = ( ( p.Y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin ).ToString();
label3.Text = null;
label4.Text = null;
return;
}
// カーソルが示している場所の座標を取得
label3.Text = ( (p.X - Xmin) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin ).ToString();
label4.Text = ( (p.Y - Ymin) * (Imax - Imin) / (Ymax - Ymin) + Imin ).ToString();
}
private void GetRegion(Point p1, Point p2, ref Point start, ref Point end)
{
start.X = Math.Min(p1.X, p2.X);
start.Y = Math.Min(p1.Y, p2.Y);
end.X = Math.Max(p1.X, p2.X);
end.Y = Math.Max(p1.Y, p2.Y);
if (checkBox1.Checked == true) //選択領域を正方形にする
{
int min_x_y = Math.Min(Math.Abs(end.X - start.X), Math.Abs(end.Y - start.Y));
end.X = start.X + min_x_y;
end.Y = start.Y + min_x_y;
}
Rmax2 = ( end.X - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin; // pictureBoxの座標を複素平面Zの座標に変換
Imax2 = ( end.Y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin;
Rmin2 = ( start.X - Xmin ) * (Rmax - Rmin) / (Xmax - Xmin) + Rmin;
Imin2 = ( start.Y - Ymin ) * (Imax - Imin) / (Ymax - Ymin) + Imin;
}
private int GetLength(int start, int end)
{
return Math.Abs(start - end);
}
private void DrawRegion(Point start, Point end)
{
Pen blackPen = new Pen(Color.White);
SolidBrush tbrush = new SolidBrush(Color.FromArgb(100,220,220,220));
// 描画する線を点線に設定
// blackPen.DashStyle = System.Drawing.Drawing2D.DashStyle.Dash;
// 画面を消去
// g.Clear(SystemColors.Control);
// 領域を描画
g.DrawRectangle(blackPen, start.X, start.Y, GetLength(start.X, end.X), GetLength(start.Y, end.Y));
g.FillRectangle(tbrush, start.X, start.Y, GetLength(start.X, end.X), GetLength(start.Y, end.Y));
}
private void button5_Click(object sender, EventArgs e)
{
// 座標を初期値に戻す
Rmax2 = 0.5;
Rmin2 = -0.5;
Imax2 = 0.5;
Imin2 = -0.5;
label1.Text = null;
label2.Text = null;
label3.Text = null;
label4.Text = null;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
}
- 座標のスケールの拡大、縮小ボタンを付ける
private void button6_Click(object sender, EventArgs e)
{
// 座標のスケールを5倍にする
double ratio = 5.0;
double R_ave = ( Rmax2 + Rmin2 ) / 2;
double R_dif2 = ( Rmax2 - Rmin2 ) / 2;
double I_ave = ( Imax2 + Imin2 ) / 2;
double I_dif2 = ( Imax2 - Imin2 ) / 2;
Rmax2 = R_ave + R_dif2 * ratio;
Rmin2 = R_ave - R_dif2 * ratio;
Imax2 = I_ave + I_dif2 * ratio;
Imin2 = I_ave - I_dif2 * ratio;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
}
private void button7_Click(object sender, EventArgs e)
{
// 座標のスケールを5分の1倍にする
double ratio = 5.0;
double R_ave = (Rmax2 + Rmin2) / 2;
double R_dif2 = (Rmax2 - Rmin2) / 2;
double I_ave = (Imax2 + Imin2) / 2;
double I_dif2 = (Imax2 - Imin2) / 2;
Rmax2 = R_ave + R_dif2 / ratio;
Rmin2 = R_ave - R_dif2 / ratio;
Imax2 = I_ave + I_dif2 / ratio;
Imin2 = I_ave - I_dif2 / ratio;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
}
- 座標の上下左右へシフトさせるボタンを付ける
private void button8_Click(object sender, EventArgs e)
{
// 座標のスケールを左に0.5スケールシフトする
double R_ave = (Rmax2 + Rmin2) * 0.5;
double R_dif2 = (Rmax2 - Rmin2) * 0.5;
Rmax2 = Rmax2 - R_dif2;
Rmin2 = Rmin2 - R_dif2;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
}
private void button9_Click(object sender, EventArgs e)
{
// 座標のスケールを右に0.5スケールシフトする
double R_ave = (Rmax2 + Rmin2) * 0.5;
double R_dif2 = (Rmax2 - Rmin2) * 0.5;
Rmax2 = Rmax2 + R_dif2;
Rmin2 = Rmin2 + R_dif2;
label5.Text = Rmax2.ToString();
label6.Text = Rmin2.ToString();
}
private void button10_Click(object sender, EventArgs e)
{
// 座標のスケールを下に0.5スケールシフトする
double I_ave = (Imax2 + Imin2) * 0.5 ;
double I_dif2 = (Imax2 - Imin2) * 0.5;
Imax2 = Imax2 - I_dif2;
Imin2 = Imin2 - I_dif2;
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
}
private void button11_Click(object sender, EventArgs e)
{
// 座標のスケールを上に0.5スケールシフトする
double I_ave = (Imax2 + Imin2) * 0.5;
double I_dif2 = (Imax2 - Imin2) * 0.5;
Imax2 = Imax2 + I_dif2;
Imin2 = Imin2 + I_dif2;
label7.Text = Imax2.ToString();
label8.Text = Imin2.ToString();
}
[編集] 人間の感覚
[編集] アロマアート
嗅覚を利用したアート
かんたん掲示板に「香りの特徴」を書いてみよう。
- 香りの印刷
- アロマプリンタ
- 映画RAMPO
- ブンマー・モンティエン,呼吸の家
- 彫刻の中に入ってハーブの香りを体感するもの (東京都現代美術館) http://www.tokyoartbeat.com/tablog/images/ShowMeThai3.jpg
- アムラックスシアター
- シーンに合わせた座席の振動・香りつきのシアター(トヨタ・アムラックス)
[編集] 共感覚
- 色彩と調性の関係性についての実験サイト(久原ゼミの実験企画)
- 色聴は共感覚(関西学院理工学部情報科学科の長田典子先生の研究室)
[編集] ヒーリングアート
- リラックスとリフレッシュ
- リラックス時には副交感神経が優勢に,興奮状態にある場合は、交感神経が優勢になる。
- リラックス時にはアルファ波が出る?
- 1/f揺らぎ
- ホワイトノイズ、サイン波、ピンクノイズ(1/f揺らぎ)
- 自然界の音を使用した楽曲 URL
- スペクトル
- EQ(イコライザ)によって,音のスペクトルを加工する。
- スペクトルとは周波数構成のこと。ピッチ感のある音は,ピークとなる基本周波数を中心として複数の倍音成分から構成される。
- SoundEngineやAudacityでsin波などを生成し,周波数構成を観察。sin波は基本周波数1つのみ。ノコギリ波はsin波の倍数の無限級数。ホワイトノイズはランダムな周波数構成。
- 人のボーカル,楽器の音,車のエンジン音のスペクトルを比較してみる。
- 子守唄
- 生物的なシステム,生物の癒し効果
flash effects / Levitated the Exploration of Computation / sodaplay/ Vector Park / リヴリー・アイランド / エレクトロプランクトン / たまごっちプラス / メンタルコミットロボアザラシ型「パロ」 / 猫型コミュニケーションロボット「ネコロ」 / nintendogs / What is TRUTH? /
- Vector Parkのegg.swf
- CLAMBON FARM
- flOw
- 電子ペット Comたま URL / PDF
[編集] 脳
[編集] Neural Networks
[編集] Genetic Algorithm
[編集] Github
共同開発するときに便利。
学内のプロキシー環境で作業する場合、コンソールで
git config --global http.proxy proxy-n.t-kougei.ac.jp:8080 git config --global https.proxy proxy-n.t-kougei.ac.jp:8080
とする。
通常のプロキシーのない環境で作業する場合、コンソールで
git config --global --unset http.proxy proxy-n.t-kougei.ac.jp:8080 git config --global --unset https.proxy proxy-n.t-kougei.ac.jp:8080
とする。
現在の設定を確認するには、コンソールで、
git config --list
とする。
[編集] リンク
素数のグラフィック http://www.datapointed.net/visualizations/math/factorization/animated-diagrams/?infinity