反応拡散系
提供:kuhalaboWiki
(版間での差分)
(→Gray-Scott Reaction-Diffusion(反応拡散系)モデル) |
(→初期状態の発生箇所をウィンドウ全体内でランダムにする) |
||
| (1人の利用者による、間の42版が非表示) | |||
| 1行: | 1行: | ||
| − | == Gray-Scott Reaction | + | == Gray-Scott Reaction and Diffusion(反応拡散系)モデル == |
| − | + | ;参照資料 | |
| − | + | * [https://www.karlsims.com/rd.html Reaction-Diffusion Tutorial] | |
| − | ; | + | * [https://mrob.com/pub/comp/xmorphia/ogl/index.html WebGL Gray-Scott Explorer] |
| − | * https://www.karlsims.com/rd.html | + | |
| − | * https://mrob.com/pub/comp/xmorphia/ogl/index.html | + | |
| − | + | ||
* http://pmneila.github.io/jsexp/grayscott/ | * http://pmneila.github.io/jsexp/grayscott/ | ||
| − | ; | + | * [https://www.t-kougei.ac.jp/activity/extension/festa2020/ 芸術学部フェスタ2020] [https://youtu.be/jZLIpPs4zYw 「反応と拡散」] / [https://www.youtube.com/watch?v=cGF8EZ2W5mA Inspiration Creation] |
| + | |||
| + | ;github | ||
* https://github.com/MStrandh/gray_scott_reaction_diffusion | * https://github.com/MStrandh/gray_scott_reaction_diffusion | ||
* https://github.com/Nekodigi/Reaction-Diffusion-Algorithm | * https://github.com/Nekodigi/Reaction-Diffusion-Algorithm | ||
| − | |||
| − | |||
| + | |||
| + | ===概要=== | ||
| + | 物質は空間内で濃度の濃いところから薄いところへ拡散し、最終的に均一になります。 | ||
| + | 2つの物質が反応しながら拡散するとき、物質の濃淡の波ができ、生物に見られる多種多様な模様が生成されます。 | ||
| + | これはチューリングパターンとして知られていて、シマウマの縞模様やヒョウの斑模様などがよい例です。 | ||
| + | |||
| + | ;反応と拡散のアルゴリズム | ||
| + | * 物質A:一定の割合で発生する('''Feed''') | ||
| + | * 物質B:一定の割合で消滅する('''Kill''') | ||
| + | * 1つのAと2つのBとが反応するとAがBに変化する。 | ||
| + | |||
| + | [[ファイル:Rd-reaction.png]] | ||
| + | |||
| + | ;反応拡散方程式 | ||
| + | * 2つの物質AとBが反応しながら、空間に拡散していく様子を反応拡散方程式で表わす。 | ||
| + | * '''Laplacian'''(ラプラシアン) = (上下左右の4方向から流入する量) - (4方向に流出する量) | ||
| + | |||
| + | [[ファイル:Rd-diffusion.png]] | ||
| + | [[ファイル:Rd-equation.png]] | ||
| + | |||
| + | ;描画 | ||
| + | * 物質A,Bの濃淡を模様として描画する。 | ||
| + | * 物質Aの発生率と物質Bの消滅率を微妙に変化させるだけで、現れる模様は大きく変化する。 | ||
| + | |||
| + | [[ファイル:Rd-grid-cells.png]] | ||
| + | |||
| + | === ソース例 === | ||
<pre> | <pre> | ||
| − | int M = | + | int M = 400; |
| − | int N = | + | int N = 400; |
//System parameters | //System parameters | ||
| − | double diffU; | + | double diffU; // U(A) diffuse rate |
| − | double diffV; | + | double diffV; // V(B) diffuse rate |
| − | double paramF; | + | double paramF; // Feed rate |
| − | double paramK; | + | double paramK; // Kill rate |
boolean rndInitCondition; | boolean rndInitCondition; | ||
| 31行: | 55行: | ||
double[][] dU = new double[M][N]; | double[][] dU = new double[M][N]; | ||
double[][] dV = new double[M][N]; | double[][] dV = new double[M][N]; | ||
| − | |||
| − | |||
void settings() { | void settings() { | ||
| 65行: | 87行: | ||
void setup() { | void setup() { | ||
frameRate(48); | frameRate(48); | ||
| − | + | // smooth(); Processing 4以降ではエラーになる | |
colorMode(HSB,1.0); | colorMode(HSB,1.0); | ||
| 71行: | 93行: | ||
diffU = 0.16; | diffU = 0.16; | ||
diffV = 0.08; | diffV = 0.08; | ||
| − | paramF = 0. | + | paramF = 0.0545; |
| − | paramK = 0. | + | paramK = 0.062; |
rndInitCondition = true; | rndInitCondition = true; | ||
| 78行: | 100行: | ||
//Populate U and V with initial data | //Populate U and V with initial data | ||
generateInitialState(); | generateInitialState(); | ||
| − | |||
} | } | ||
| − | void timestep( | + | void timestep() { |
for (int i = 0; i < M; i++) { | for (int i = 0; i < M; i++) { | ||
for (int j = 0; j < N; j++) { | for (int j = 0; j < N; j++) { | ||
| − | + | // int p = i + j*N; | |
double u = U[i][j]; | double u = U[i][j]; | ||
double v = V[i][j]; | double v = V[i][j]; | ||
| − | |||
| − | |||
double uvv = u*v*v; | double uvv = u*v*v; | ||
| 100行: | 119行: | ||
double lapV = (V[left][j] + V[right][j] + V[i][up] + V[i][down] - 4*v); | double lapV = (V[left][j] + V[right][j] + V[i][up] + V[i][down] - 4*v); | ||
| − | dU[i][j] = diffU*lapU - uvv + | + | dU[i][j] = diffU*lapU - uvv + paramF*(1 - u); |
| − | dV[i][j] = diffV*lapV + uvv - ( | + | dV[i][j] = diffV*lapV + uvv - (paramK+paramF)*v; |
} | } | ||
} | } | ||
| − | |||
| − | |||
for (int i= 0; i < M; i++) { | for (int i= 0; i < M; i++) { | ||
for (int j = 0; j < N; j++){ | for (int j = 0; j < N; j++){ | ||
| 115行: | 132行: | ||
void draw(){ | void draw(){ | ||
| − | for (int | + | for (int i = 0; i < 20; i++) { |
| − | timestep( | + | timestep(); |
} | } | ||
| 123行: | 140行: | ||
for (int j = 0; j < N; j++) { | for (int j = 0; j < N; j++) { | ||
set(i, j, color((float)(1-U[i][j]),0.9, 0.5 )); | set(i, j, color((float)(1-U[i][j]),0.9, 0.5 )); | ||
| − | |||
| − | |||
} | } | ||
} | } | ||
} | } | ||
| + | </pre> | ||
| + | === キーボードでパラメータを変更 === | ||
| + | <pre> | ||
void keyPressed() { | void keyPressed() { | ||
switch (key) { | switch (key) { | ||
| 191行: | 209行: | ||
} | } | ||
</pre> | </pre> | ||
| + | |||
| + | === 初期状態の発生箇所をウィンドウ全体内でランダムにする === | ||
| + | <pre> | ||
| + | void generateInitialState() { | ||
| + | for (int i = 0; i < M; i++) { | ||
| + | for (int j = 0; j < N; j++) { | ||
| + | U[i][j] = 1.0; | ||
| + | V[i][j] = 0.0; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | if (rndInitCondition) { | ||
| + | for (int i = 0; i < M; i++) { | ||
| + | for (int j = 0; j < N; j++) { | ||
| + | U[i][j] = 0.5*(1 + random(-1, 1)); | ||
| + | V[i][j] = 0.25*( 1 + random(-1, 1)); | ||
| + | } | ||
| + | } | ||
| + | } else { | ||
| + | for (int i = 0; i < M; i++) { | ||
| + | for (int j = 0; j < N; j++) { | ||
| + | U[i][j] = 0.5; | ||
| + | V[i][j] = 0.25; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | === 模様の発生場所を特定の矩形内に限定する === | ||
| + | *発生領域 | ||
| + | **X軸:M1からM2 | ||
| + | **Y軸:N1からN2 | ||
| + | |||
| + | <pre> | ||
| + | int M1 = 200; | ||
| + | int N1 = 300; | ||
| + | int M2 = 600; | ||
| + | int N2 = 500; | ||
| + | </pre> | ||
| + | |||
| + | <pre> | ||
| + | void timestep() { | ||
| + | for (int i = M1; i < M2; i++) { | ||
| + | for (int j = N1; j < N2; j++) { | ||
| + | // int p = i + j*N; | ||
| + | |||
| + | double u = U[i][j]; | ||
| + | double v = V[i][j]; | ||
| + | double uvv = u*v*v; | ||
| + | |||
| + | int left = (i-1+M2) % M2; | ||
| + | int right = (i+1) % M2; | ||
| + | int up = (j-1+N2) % N2; | ||
| + | int down = (j+1) % N2; | ||
| + | |||
| + | double lapU = (U[left][j] + U[right][j] + U[i][up] + U[i][down] - 4*u); | ||
| + | double lapV = (V[left][j] + V[right][j] + V[i][up] + V[i][down] - 4*v); | ||
| + | |||
| + | dU[i][j] = diffU*lapU - uvv + paramF*(1 - u); | ||
| + | dV[i][j] = diffV*lapV + uvv - (paramK+paramF)*v; | ||
| + | } | ||
| + | } | ||
| + | for (int i= 0; i < M; i++) { | ||
| + | for (int j = 0; j < N; j++){ | ||
| + | U[i][j] += dU[i][j]; | ||
| + | V[i][j] += dV[i][j]; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | == 人工生命(ALife) == | ||
| + | |||
| + | [[セルオートマトン]] | ||
| + | |||
| + | [[ラングトンのアリ]] | ||
| + | |||
| + | [[レイノルズのボイド]] | ||
| + | |||
| + | [[フラクタル]] | ||
== 参考 == | == 参考 == | ||
2024年12月4日 (水) 05:45時点における最新版
目次 |
[編集] Gray-Scott Reaction and Diffusion(反応拡散系)モデル
- 参照資料
- Reaction-Diffusion Tutorial
- WebGL Gray-Scott Explorer
- http://pmneila.github.io/jsexp/grayscott/
- 芸術学部フェスタ2020 「反応と拡散」 / Inspiration Creation
- github
- https://github.com/MStrandh/gray_scott_reaction_diffusion
- https://github.com/Nekodigi/Reaction-Diffusion-Algorithm
[編集] 概要
物質は空間内で濃度の濃いところから薄いところへ拡散し、最終的に均一になります。 2つの物質が反応しながら拡散するとき、物質の濃淡の波ができ、生物に見られる多種多様な模様が生成されます。 これはチューリングパターンとして知られていて、シマウマの縞模様やヒョウの斑模様などがよい例です。
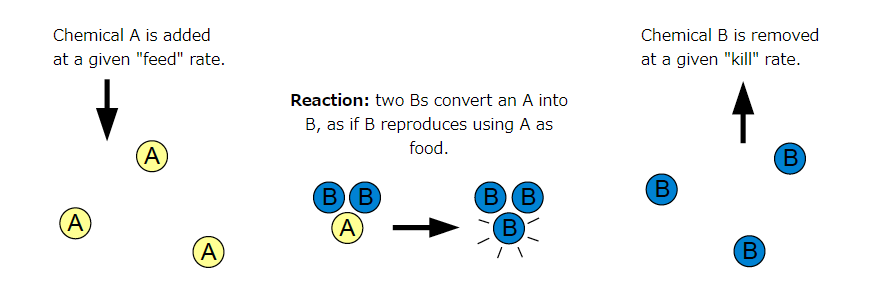
- 反応と拡散のアルゴリズム
- 物質A:一定の割合で発生する(Feed)
- 物質B:一定の割合で消滅する(Kill)
- 1つのAと2つのBとが反応するとAがBに変化する。
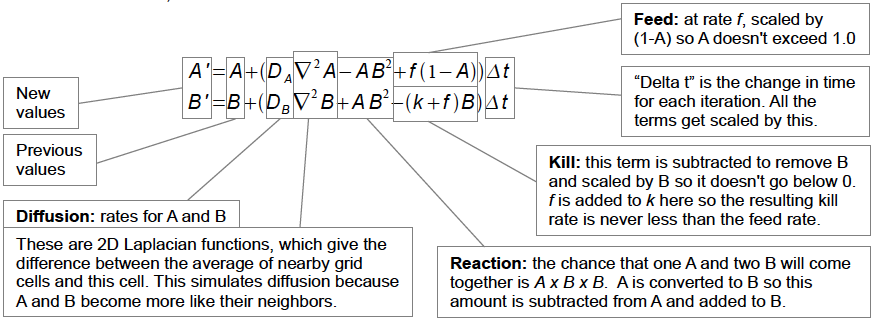
- 反応拡散方程式
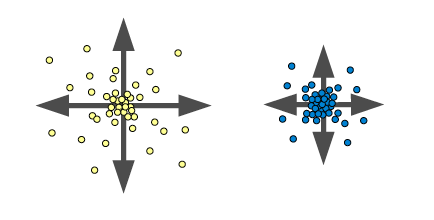
- 2つの物質AとBが反応しながら、空間に拡散していく様子を反応拡散方程式で表わす。
- Laplacian(ラプラシアン) = (上下左右の4方向から流入する量) - (4方向に流出する量)
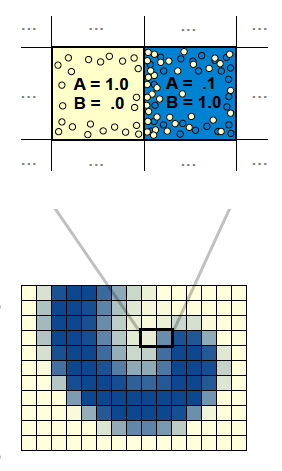
- 描画
- 物質A,Bの濃淡を模様として描画する。
- 物質Aの発生率と物質Bの消滅率を微妙に変化させるだけで、現れる模様は大きく変化する。
[編集] ソース例
int M = 400;
int N = 400;
//System parameters
double diffU; // U(A) diffuse rate
double diffV; // V(B) diffuse rate
double paramF; // Feed rate
double paramK; // Kill rate
boolean rndInitCondition;
double[][] U = new double[M][N];
double[][] V = new double[M][N];
double[][] dU = new double[M][N];
double[][] dV = new double[M][N];
void settings() {
size(M,N);
}
void generateInitialState() {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
U[i][j] = 1.0;
V[i][j] = 0.0;
}
}
if (rndInitCondition) {
for (int i = M/3; i < 2*M/3; i++) {
for (int j = N/3; j < 2*N/3; j++) {
U[i][j] = 0.5*(1 + random(-1, 1));
V[i][j] = 0.25*( 1 + random(-1, 1));
}
}
} else {
for (int i = M/3; i < 2*M/3; i++) {
for (int j = N/3; j < 2*N/3; j++) {
U[i][j] = 0.5;
V[i][j] = 0.25;
}
}
}
}
void setup() {
frameRate(48);
// smooth(); Processing 4以降ではエラーになる
colorMode(HSB,1.0);
//Set default parameters;
diffU = 0.16;
diffV = 0.08;
paramF = 0.0545;
paramK = 0.062;
rndInitCondition = true;
//Populate U and V with initial data
generateInitialState();
}
void timestep() {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
// int p = i + j*N;
double u = U[i][j];
double v = V[i][j];
double uvv = u*v*v;
int left = (i-1+M) % M;
int right = (i+1) % M;
int up = (j-1+N) % N;
int down = (j+1) % N;
double lapU = (U[left][j] + U[right][j] + U[i][up] + U[i][down] - 4*u);
double lapV = (V[left][j] + V[right][j] + V[i][up] + V[i][down] - 4*v);
dU[i][j] = diffU*lapU - uvv + paramF*(1 - u);
dV[i][j] = diffV*lapV + uvv - (paramK+paramF)*v;
}
}
for (int i= 0; i < M; i++) {
for (int j = 0; j < N; j++){
U[i][j] += dU[i][j];
V[i][j] += dV[i][j];
}
}
}
void draw(){
for (int i = 0; i < 20; i++) {
timestep();
}
// Draw points
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
set(i, j, color((float)(1-U[i][j]),0.9, 0.5 ));
}
}
}
[編集] キーボードでパラメータを変更
void keyPressed() {
switch (key) {
case '1':
diffU = 0.16;
diffV = 0.08;
paramF = 0.035;
paramK = 0.06;
generateInitialState();
break;
case '2':
diffU = 0.16;
diffV = 0.08;
paramF = 0.042;
paramK = 0.065;
generateInitialState();
break;
case '3':
diffU = 0.18;
diffV = 0.13;
paramF = 0.025;
paramK = 0.056;
generateInitialState();
break;
case '4':
diffU = 0.18;
diffV = 0.09;
paramF = 0.02;
paramK = 0.056;
generateInitialState();
break;
case '5':
diffU = 0.14;
diffV = 0.06;
paramF = 0.035;
paramK = 0.065;
generateInitialState();
break;
case '6':
diffU = 0.19;
diffV = 0.09;
paramF = 0.062;
paramK = 0.062;
generateInitialState();
break;
case '7':
diffU = 0.16;
diffV = 0.08;
paramF = 0.05;
paramK = 0.065;
generateInitialState();
break;
case 'r':
rndInitCondition = true;
generateInitialState();
break;
case 'n':
rndInitCondition = false;
generateInitialState();
}
}
[編集] 初期状態の発生箇所をウィンドウ全体内でランダムにする
void generateInitialState() {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
U[i][j] = 1.0;
V[i][j] = 0.0;
}
}
if (rndInitCondition) {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
U[i][j] = 0.5*(1 + random(-1, 1));
V[i][j] = 0.25*( 1 + random(-1, 1));
}
}
} else {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
U[i][j] = 0.5;
V[i][j] = 0.25;
}
}
}
}
[編集] 模様の発生場所を特定の矩形内に限定する
- 発生領域
- X軸:M1からM2
- Y軸:N1からN2
int M1 = 200; int N1 = 300; int M2 = 600; int N2 = 500;
void timestep() {
for (int i = M1; i < M2; i++) {
for (int j = N1; j < N2; j++) {
// int p = i + j*N;
double u = U[i][j];
double v = V[i][j];
double uvv = u*v*v;
int left = (i-1+M2) % M2;
int right = (i+1) % M2;
int up = (j-1+N2) % N2;
int down = (j+1) % N2;
double lapU = (U[left][j] + U[right][j] + U[i][up] + U[i][down] - 4*u);
double lapV = (V[left][j] + V[right][j] + V[i][up] + V[i][down] - 4*v);
dU[i][j] = diffU*lapU - uvv + paramF*(1 - u);
dV[i][j] = diffV*lapV + uvv - (paramK+paramF)*v;
}
}
for (int i= 0; i < M; i++) {
for (int j = 0; j < N; j++){
U[i][j] += dU[i][j];
V[i][j] += dV[i][j];
}
}
}