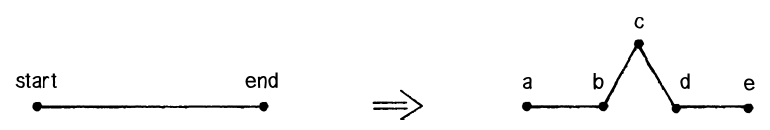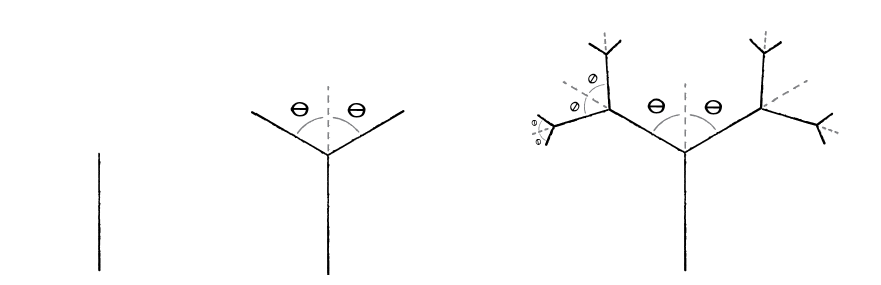フラクタル
提供:kuhalaboWiki
(版間での差分)
(→コッホ図形) |
(→参考) |
||
| (1人の利用者による、間の43版が非表示) | |||
| 1行: | 1行: | ||
| − | == | + | == 自己相似形 == |
| + | ;フラクタル(fractal) | ||
| + | :フランスの数学者ブノワ・マンデルブロが導入した幾何学の概念である。ラテン語の fractus から。図形の部分と全体が自己相似(再帰)になっているものなどをいう。 | ||
| + | |||
| + | ;古代ギリシャからあるユークリッド幾何学と20世紀のフラクタル幾何学の比較 | ||
| + | :人工物は、直線、円などユークリッド幾何学で設計されることが多い。 | ||
| + | :自然界には自己相似なフラクタル幾何学で記述できるものが多い。 | ||
| + | ::例 海岸線、樹木、雪の結晶、貝、台風、銀河... | ||
| + | :: [https://www.jw.org/ja/%E3%83%A9%E3%82%A4%E3%83%96%E3%83%A9%E3%83%AA%E3%83%BC/%E3%83%93%E3%83%87%E3%82%AA/%E5%89%B5%E9%80%A0%E3%81%AE%E9%A9%9A%E7%95%B0%E3%81%AF%E7%A5%9E%E3%81%AE%E6%A0%84%E5%85%89%E3%82%92%E8%A1%A8%E3%82%8F%E3%81%99/%E3%83%91%E3%82%BF%E3%83%BC%E3%83%B3/ 創造の驚異は神の栄光を表す「パターン」] | ||
| + | |||
[https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%AB フラクタル wikipedia] | [https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%AB フラクタル wikipedia] | ||
| − | + | ;フラクタル図形を応用した例 | |
| − | + | ||
| − | ; | + | |
| − | + | ||
| − | + | ||
[http://www.gaia.h.kyoto-u.ac.jp/~fractal/ フラクタル日除け] | [http://www.gaia.h.kyoto-u.ac.jp/~fractal/ フラクタル日除け] | ||
| − | + | [http://ariga.dwcmedia.jp/ProcessingWeb/TrailGeneral.html フラクタルを描く] | |
| − | + | ||
== 再帰的呼び出し == | == 再帰的呼び出し == | ||
| − | |||
再帰的(recursive)呼び出しとは,サブルーチンや関数が,自分自身を呼び出すアルゴリズムをいう。 | 再帰的(recursive)呼び出しとは,サブルーチンや関数が,自分自身を呼び出すアルゴリズムをいう。 | ||
これを利用すると,複雑な手順を簡潔に記述することができる。 | これを利用すると,複雑な手順を簡潔に記述することができる。 | ||
| 30行: | 33行: | ||
: n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1 | : n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1 | ||
: 1! = 1 | : 1! = 1 | ||
| − | + | : n! = n * (n-1)! とも書ける(再帰的な定義) | |
| + | |||
| + | ;再帰 n!=n*(n-1)! という漸化式で計算する。 | ||
<pre> | <pre> | ||
| − | |||
int factorial(int n){ | int factorial(int n){ | ||
if (n == 1){ | if (n == 1){ | ||
| 40行: | 44行: | ||
} | } | ||
} | } | ||
| + | </pre> | ||
| − | + | ;反復 1からnまでを乗算する。 | |
| + | <pre> | ||
int factorial(int n){ | int factorial(int n){ | ||
int f = 1; | int f = 1; | ||
| 52行: | 58行: | ||
== 再帰的な円 == | == 再帰的な円 == | ||
| − | + | ;Nature of Code, Ch 8 Fractals | |
| + | : https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals | ||
<pre> | <pre> | ||
| 81行: | 88行: | ||
== コッホ図形 == | == コッホ図形 == | ||
| − | [[ファイル: | + | 直線を3等分して、中央に正三角形を描く。 |
| − | [[ファイル: | + | |
| + | [[ファイル:Koch01.png]] | ||
| + | |||
| + | 上記の操作を4回繰り返す。 | ||
| + | |||
| + | [[ファイル:Koch02.png]] | ||
| + | |||
| + | === ソース例 === | ||
| + | |||
| + | * https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals/NOC_8_05_KochSimple | ||
| − | |||
<pre> | <pre> | ||
| + | // Koch Curve | ||
// Renders a simple fractal, the Koch snowflake | // Renders a simple fractal, the Koch snowflake | ||
// Each recursive level drawn in sequence | // Each recursive level drawn in sequence | ||
| − | + | ArrayList<KochLine> lines ; // A list to keep track of all the lines | |
void setup() { | void setup() { | ||
| − | size( | + | size(383, 200); |
background(255); | background(255); | ||
| − | + | lines = new ArrayList<KochLine>(); | |
| − | + | PVector start = new PVector(0, 150); | |
| + | PVector end = new PVector(width, 150); | ||
| + | lines.add(new KochLine(start, end)); | ||
| + | |||
| + | for (int i = 0; i < 5; i++) { | ||
| + | generate(); | ||
| + | } | ||
| + | |||
| + | smooth(); | ||
} | } | ||
void draw() { | void draw() { | ||
background(255); | background(255); | ||
| − | + | for (KochLine l : lines) { | |
| − | + | l.display(); | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
} | } | ||
} | } | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | void generate() { | |
| − | // | + | ArrayList next = new ArrayList<KochLine>(); // Create emtpy list |
| − | // | + | for (KochLine l : lines) { |
| − | + | // Calculate 5 koch PVectors (done for us by the line object) | |
| − | + | PVector a = l.kochA(); | |
| + | PVector b = l.kochB(); | ||
| + | PVector c = l.kochC(); | ||
| + | PVector d = l.kochD(); | ||
| + | PVector e = l.kochE(); | ||
| + | // Make line segments between all the PVectors and add them | ||
| + | next.add(new KochLine(a, b)); | ||
| + | next.add(new KochLine(b, c)); | ||
| + | next.add(new KochLine(c, d)); | ||
| + | next.add(new KochLine(d, e)); | ||
} | } | ||
| + | lines = next; | ||
| + | } | ||
| + | </pre> | ||
| − | + | === KochLineクラス=== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | * 5つの点'''a,b,c,d,e'''を得る。 | |
| − | + | [[ファイル:Koch03.png]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | * 点'''b'''は、ベクトル'''AE'''の1/3 | |
| − | + | * 点'''d'''は、ベクトル'''AE'''の2/3 | |
| + | * 点'''c'''は、点'''b'''を中心に点'''d'''を60度回転 | ||
| + | [[ファイル:Koch04.png]] | ||
| − | |||
<pre> | <pre> | ||
| + | |||
// Koch Curve | // Koch Curve | ||
// A class to describe one line segment in the fractal | // A class to describe one line segment in the fractal | ||
| 192行: | 169行: | ||
// a is the "left" PVector and | // a is the "left" PVector and | ||
// b is the "right PVector | // b is the "right PVector | ||
| − | PVector | + | PVector start; |
| − | PVector | + | PVector end; |
| − | KochLine(PVector | + | KochLine(PVector a, PVector b) { |
| − | + | start = a.get(); | |
| − | + | end = b.get(); | |
} | } | ||
void display() { | void display() { | ||
stroke(0); | stroke(0); | ||
| − | line( | + | line(start.x, start.y, end.x, end.y); |
} | } | ||
| − | PVector | + | PVector kochA() { |
| − | return | + | return start.get(); |
} | } | ||
| − | |||
| − | |||
| − | |||
// This is easy, just 1/3 of the way | // This is easy, just 1/3 of the way | ||
| − | PVector | + | PVector kochB() { |
| − | PVector v = PVector.sub( | + | PVector v = PVector.sub(end, start); |
v.div(3); | v.div(3); | ||
| − | v.add( | + | v.add(start); |
return v; | return v; | ||
} | } | ||
// More complicated, have to use a little trig to figure out where this PVector is! | // More complicated, have to use a little trig to figure out where this PVector is! | ||
| − | PVector | + | PVector kochC() { |
| − | PVector | + | PVector a = start.get(); // Start at the beginning |
| − | + | ||
| − | PVector | + | PVector v = PVector.sub(end, start); |
| − | + | v.div(3); | |
| − | + | a.add(v); // Move to point B | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | v.rotate(-radians(60)); // Rotate 60 degrees | ||
| + | a.add(v); // Move to point C | ||
| + | |||
| + | return a; | ||
| + | } | ||
// Easy, just 2/3 of the way | // Easy, just 2/3 of the way | ||
| − | PVector | + | PVector kochD() { |
| − | PVector v = PVector.sub( | + | PVector v = PVector.sub(end, start); |
| − | v. | + | v.mult(2/3.0); |
| − | v.add( | + | v.add(start); |
return v; | return v; | ||
| + | } | ||
| + | |||
| + | PVector kochE() { | ||
| + | return end.get(); | ||
} | } | ||
} | } | ||
| + | </pre> | ||
| + | |||
| + | ===応用例=== | ||
| + | * https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals/NOC_8_05_Koch | ||
| + | * https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals/Exercise_8_02_KochSnowFlake | ||
| + | |||
| + | == 樹木 == | ||
| + | |||
| + | [[ファイル:Tree03.png]] | ||
| + | |||
| + | [[ファイル:Tree01.png]] | ||
| + | |||
| + | [[ファイル:Tree02.png]] | ||
| + | |||
| + | ==== シンプルな例 ==== | ||
| + | |||
| + | https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals/Exercise_8_06_Tree | ||
| + | |||
| + | <pre> | ||
| + | // The Nature of Code | ||
| + | // Daniel Shiffman | ||
| + | // http://natureofcode.com | ||
| + | |||
| + | // Recursive Tree | ||
| + | |||
| + | // Renders a simple tree-like structure via recursion | ||
| + | // Branching angle calculated as a function of horizontal mouse position | ||
| + | |||
| + | float theta; | ||
| + | |||
| + | void setup() { | ||
| + | size(1800, 500); | ||
| + | smooth(); | ||
| + | } | ||
| + | |||
| + | void draw() { | ||
| + | background(255); | ||
| + | // Let's pick an angle 0 to 90 degrees based on the mouse position | ||
| + | theta = PI/6;//map(mouseX,0,width,0,PI/2); | ||
| + | |||
| + | // Start the tree from the bottom of the screen | ||
| + | translate(width/2, height); | ||
| + | stroke(0); | ||
| + | branch(200,0); | ||
| + | save("chapter08_exc06.png"); | ||
| + | noLoop(); | ||
| + | } | ||
| + | |||
| + | void branch(float len, int level) { | ||
| + | // Each branch will be 2/3rds the size of the previous one | ||
| + | |||
| + | //float sw = map(len,2,120,1,10); | ||
| + | //strokeWeight(sw); | ||
| + | strokeWeight(2); | ||
| + | |||
| + | line(0, 0, 0, -len); | ||
| + | // Move to the end of that line | ||
| + | translate(0, -len); | ||
| + | |||
| + | len *= 0.66; | ||
| + | level++; | ||
| + | // All recursive functions must have an exit condition!!!! | ||
| + | // Here, ours is when the length of the branch is 2 pixels or less | ||
| + | if (level < 5) { | ||
| + | pushMatrix(); // Save the current state of transformation (i.e. where are we now) | ||
| + | rotate(theta); // Rotate by theta | ||
| + | branch(len,level); // Ok, now call myself to draw two new branches!! | ||
| + | popMatrix(); // Whenever we get back here, we "pop" in order to restore the previous matrix state | ||
| − | + | // Repeat the same thing, only branch off to the "left" this time! | |
| − | + | pushMatrix(); | |
| − | // | + | rotate(-theta); |
| − | + | branch(len,level); | |
| − | + | popMatrix(); | |
} | } | ||
| + | } | ||
</pre> | </pre> | ||
| + | |||
| + | ;様々な応用例(Nature of Code) | ||
| + | * https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals | ||
| + | |||
| + | == 人工生命(ALife) == | ||
| + | |||
| + | [[セルオートマトン]] | ||
| + | |||
| + | [[ラングトンのアリ]] | ||
| + | |||
| + | [[レイノルズのボイド]] | ||
| + | |||
| + | [[反応拡散系]] | ||
| + | |||
| + | == 参考 == | ||
| + | [[スケーラブルアート論]] | ||
| + | |||
| + | [[Category:授業]] | ||
2021年10月15日 (金) 00:25時点における最新版
目次 |
[編集] 自己相似形
- フラクタル(fractal)
- フランスの数学者ブノワ・マンデルブロが導入した幾何学の概念である。ラテン語の fractus から。図形の部分と全体が自己相似(再帰)になっているものなどをいう。
- 古代ギリシャからあるユークリッド幾何学と20世紀のフラクタル幾何学の比較
- 人工物は、直線、円などユークリッド幾何学で設計されることが多い。
- 自然界には自己相似なフラクタル幾何学で記述できるものが多い。
- 例 海岸線、樹木、雪の結晶、貝、台風、銀河...
- 創造の驚異は神の栄光を表す「パターン」
- フラクタル図形を応用した例
[編集] 再帰的呼び出し
再帰的(recursive)呼び出しとは,サブルーチンや関数が,自分自身を呼び出すアルゴリズムをいう。 これを利用すると,複雑な手順を簡潔に記述することができる。
- 再帰的(Recursive)呼び出し
- "Recursive"という言葉を「頭山的」と訳した人がいる。
- 落語「自分の頭の上に穴があいて池ができた。その人が将来を悲観して,その池に身を投げた」
- 再帰的な定義の例: GNU: " GNU is Not Unix "
再帰は数学的帰納法であり,「局所的なルールで全体を記述する」ことである。 i)最初のコマを倒す。ii)n番目のコマが倒れると,n+1番目のコマも倒れる。iii)すべてのコマが倒れる。
- nの階乗を再帰と反復で計算する際の比較
- n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1
- 1! = 1
- n! = n * (n-1)! とも書ける(再帰的な定義)
- 再帰 n!=n*(n-1)! という漸化式で計算する。
int factorial(int n){
if (n == 1){
return 1;
}else{
return n * factorial(n-1); //再帰的呼び出し
}
}
- 反復 1からnまでを乗算する。
int factorial(int n){
int f = 1;
for (int i = 0; i < n; i++){
f = f * (i+1);
}
return f;
}
[編集] 再帰的な円
- Nature of Code, Ch 8 Fractals
- https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals
void setup() {
size(640,360);
}
void draw() {
background(255);
drawCircle(width/2,height/2,400);
noLoop();
}
// Recursive function
void drawCircle(float x, float y, float r) {
stroke(0);
noFill();
ellipse(x, y, r, r);
if(r > 2) {
// Now we draw two more circles, one to the left
// and one to the right
drawCircle(x + r/2, y, r/2);
drawCircle(x - r/2, y, r/2);
}
}
[編集] コッホ図形
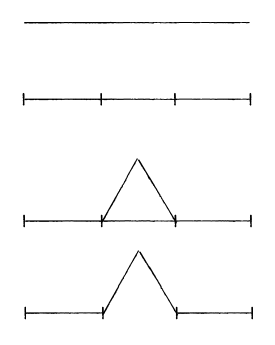
直線を3等分して、中央に正三角形を描く。
上記の操作を4回繰り返す。
[編集] ソース例
// Koch Curve
// Renders a simple fractal, the Koch snowflake
// Each recursive level drawn in sequence
ArrayList<KochLine> lines ; // A list to keep track of all the lines
void setup() {
size(383, 200);
background(255);
lines = new ArrayList<KochLine>();
PVector start = new PVector(0, 150);
PVector end = new PVector(width, 150);
lines.add(new KochLine(start, end));
for (int i = 0; i < 5; i++) {
generate();
}
smooth();
}
void draw() {
background(255);
for (KochLine l : lines) {
l.display();
}
}
void generate() {
ArrayList next = new ArrayList<KochLine>(); // Create emtpy list
for (KochLine l : lines) {
// Calculate 5 koch PVectors (done for us by the line object)
PVector a = l.kochA();
PVector b = l.kochB();
PVector c = l.kochC();
PVector d = l.kochD();
PVector e = l.kochE();
// Make line segments between all the PVectors and add them
next.add(new KochLine(a, b));
next.add(new KochLine(b, c));
next.add(new KochLine(c, d));
next.add(new KochLine(d, e));
}
lines = next;
}
[編集] KochLineクラス
- 5つの点a,b,c,d,eを得る。
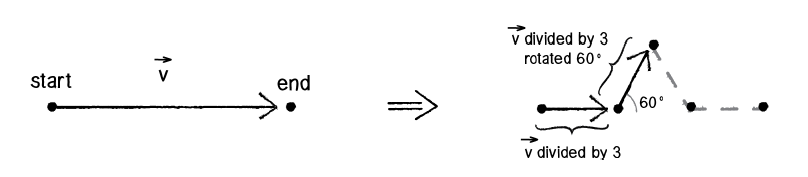
- 点bは、ベクトルAEの1/3
- 点dは、ベクトルAEの2/3
- 点cは、点bを中心に点dを60度回転
// Koch Curve
// A class to describe one line segment in the fractal
// Includes methods to calculate midPVectors along the line according to the Koch algorithm
class KochLine {
// Two PVectors,
// a is the "left" PVector and
// b is the "right PVector
PVector start;
PVector end;
KochLine(PVector a, PVector b) {
start = a.get();
end = b.get();
}
void display() {
stroke(0);
line(start.x, start.y, end.x, end.y);
}
PVector kochA() {
return start.get();
}
// This is easy, just 1/3 of the way
PVector kochB() {
PVector v = PVector.sub(end, start);
v.div(3);
v.add(start);
return v;
}
// More complicated, have to use a little trig to figure out where this PVector is!
PVector kochC() {
PVector a = start.get(); // Start at the beginning
PVector v = PVector.sub(end, start);
v.div(3);
a.add(v); // Move to point B
v.rotate(-radians(60)); // Rotate 60 degrees
a.add(v); // Move to point C
return a;
}
// Easy, just 2/3 of the way
PVector kochD() {
PVector v = PVector.sub(end, start);
v.mult(2/3.0);
v.add(start);
return v;
}
PVector kochE() {
return end.get();
}
}
[編集] 応用例
- https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals/NOC_8_05_Koch
- https://github.com/nature-of-code/noc-examples-processing/tree/master/chp08_fractals/Exercise_8_02_KochSnowFlake
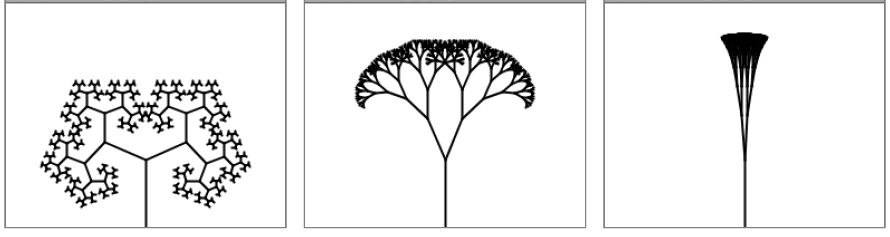
[編集] 樹木
[編集] シンプルな例
// The Nature of Code
// Daniel Shiffman
// http://natureofcode.com
// Recursive Tree
// Renders a simple tree-like structure via recursion
// Branching angle calculated as a function of horizontal mouse position
float theta;
void setup() {
size(1800, 500);
smooth();
}
void draw() {
background(255);
// Let's pick an angle 0 to 90 degrees based on the mouse position
theta = PI/6;//map(mouseX,0,width,0,PI/2);
// Start the tree from the bottom of the screen
translate(width/2, height);
stroke(0);
branch(200,0);
save("chapter08_exc06.png");
noLoop();
}
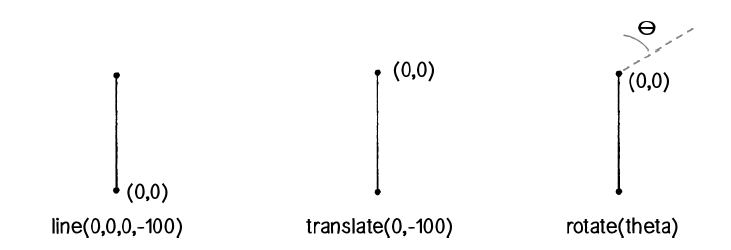
void branch(float len, int level) {
// Each branch will be 2/3rds the size of the previous one
//float sw = map(len,2,120,1,10);
//strokeWeight(sw);
strokeWeight(2);
line(0, 0, 0, -len);
// Move to the end of that line
translate(0, -len);
len *= 0.66;
level++;
// All recursive functions must have an exit condition!!!!
// Here, ours is when the length of the branch is 2 pixels or less
if (level < 5) {
pushMatrix(); // Save the current state of transformation (i.e. where are we now)
rotate(theta); // Rotate by theta
branch(len,level); // Ok, now call myself to draw two new branches!!
popMatrix(); // Whenever we get back here, we "pop" in order to restore the previous matrix state
// Repeat the same thing, only branch off to the "left" this time!
pushMatrix();
rotate(-theta);
branch(len,level);
popMatrix();
}
}
- 様々な応用例(Nature of Code)