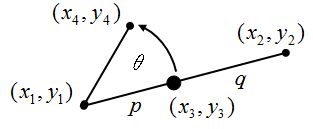生命情報アート論

提供：kuhalaboWiki
（版間での差分）
移動： 案内, 検索
(→‎小テスト)
(→‎予定)
15行： 15行：
  
 
== 予定 ==
 
== 予定 ==
 +
 +
;2013年度
 +
:担当 久原
 +
 +
# 9/24(火) ガイダンス, 生物と情報とアート，オブジェクト指向プログラミング演習
 +
# 10/1(火) C#プログラミング演習
 +
# 10/8(火) セルオートマトン
 +
# 10/15(火) 幾何学図形の描画(C#プログラミング演習)
 +
# 10/22(火) 幾何学図形の描画(C#プログラミング演習)
 +
# 10/29(火) セルオートマトンによる描画(C#演習)
 +
# 11/5(火)
 +
# 11/12(火) 
 +
# 11/19(火)
 +
# 11/26(火)
 +
# 12/3(火)
 +
# 12/10(火)
 +
# 12/17(火)
 +
# 1/7(火) 予備演習日
 +
# 1/21(火) 小テスト
 +
  
 
=== 2012年スケジュール===
 
=== 2012年スケジュール===

2013年9月23日 (月) 22:23時点における版

目次

概要

授業概要及び到達目標
メディアアートは芸術を基盤として科学や工学を統合する新しい領域である。生物科学に関連した分野として、人工生命、ライフゲーム、フラクタル、オートマトン、遺伝的アルゴリズム、ニューラルネットワークなど応用範囲の広いものが数多く存在する。人間は五感によって自然界から情報を獲得し、それと同時に自然界に対して様々な働きかけを行っている。これらは外界に発信されるメッセージである。一方、芸術とは人間が自然界に対してメッセージ性のある積極的な働きかけを行った産物に他ならない。生物の特長に注目し、新しい芸術表現の可能性について扱う。本講義の目標は以下の通り。
  1. 生物の特徴と生物的なシステムについて理解する。
  2. 複雑系システムについて理解し、応用例を作成できる。
  3. 人間の五感について考察し芸術への応用について考察する。
  4. 癒しのメカニズムについて学び芸術へ応用できる。

予定

2013年度
担当 久原
  1. 9/24(火) ガイダンス, 生物と情報とアート，オブジェクト指向プログラミング演習
  2. 10/1(火) C#プログラミング演習
  3. 10/8(火) セルオートマトン
  4. 10/15(火) 幾何学図形の描画(C#プログラミング演習)
  5. 10/22(火) 幾何学図形の描画(C#プログラミング演習)
  6. 10/29(火) セルオートマトンによる描画(C#演習)
  7. 11/5(火)
  8. 11/12(火)
  9. 11/19(火)
  10. 11/26(火)
  11. 12/3(火)
  12. 12/10(火)
  13. 12/17(火)
  14. 1/7(火) 予備演習日
  15. 1/21(火) 小テスト


2012年スケジュール

担当

久原，森山

  1. 9/14(金)生物と情報とアート，オブジェクト指向プログラミング演習
  2. 9/21(金)C#プログラミング演習
  3. 9/28(金)セルオートマトン
  4. 10/5(金)幾何学図形の描画(C#プログラミング演習)
  5. 10/12(金)幾何学図形の描画(C#演習)
  6. 10/26(金)セルオートマトンによる描画(C#演習)
  7. 11/2(金)フラクタル
  8. 11/9(金)再起呼出しによる自己相似形(C#実習)
  9. 11/16(金)再起呼出しによる自己相似形(C#実習)
  10. 11/30(金)再起呼出しによる自己相似形(C#実習)
  11. 12/7(金)複素平面フラクタル
  12. 12/14(金)遺伝的アルゴリズム、アロマアート,ヒーリングアート
  13. 12/21(金)ニューラルネットワーク,脳波,共感覚,1/f揺らぎ
  14. 1/11(金)自由制作日(出席は取りません)
  15. 1/25(金)小テスト

2011年スケジュール

担当

久原，森山

  1. 9/16(金)生物と情報とアート，オブジェクト指向プログラミング演習
  2. 9/24(土)C#プログラミング演習
  3. 9/30(金)セルオートマトン
  4. 10/7(金)幾何学図形の描画(C#プログラミング演習)
  5. 10/14(金)幾何学図形の描画(C#演習)
  6. 10/28(金)幾何学図形＆1次元セルオートマトンによる描画(C#演習)
  7. 11/4(金)フラクタル
  8. 11/11(金)再起呼出しによる自己相似形(C#実習)
  9. 11/18(金)再起呼出しによる自己相似形(C#実習)
  10. 11/25(金)再起呼出しによる自己相似形(C#実習)
  11. 12/2(金)複素平面フラクタル
  12. 12/9(金)遺伝的アルゴリズム、アロマアート,ヒーリングアート
  13. 12/16(金)ニューラルネットワーク,脳波,共感覚,1/f揺らぎ
  14. 1/6(金)自由制作日(出席は取りません)
  15. 1/20(金)小テスト

2010年スケジュール

担当
久原
  1. 9/17(金) 生物と情報とアート，オブジェクト指向プログラミング演習
  2. 9/24(金) C#プログラミング演習
  3. 10/1(金) セルオートマトン
  4. 10/8(金) 幾何学図形の描画(C#プログラミング演習)
  5. 10/15(金) 1次元セルオートマトンによる描画(C#演習)
  6. 10/22(金) 休講：工芸祭準備日
  7. 10/29(金) 1次元セルオートマトンによる描画(C#演習)
  8. 11/5(金) フラクタル
  9. 11/12(金) 再起呼出しによる自己相似形(C#実習)
  10. 11/19(金) 再起呼出しによる自己相似形(C#実習)
  11. 11/26(金) 複素平面フラクタル
  12. 12/3(金) 遺伝的アルゴリズム
  13. 12/10(金) アロマアート,ヒーリングアート
  14. 12/17(金) ニューラルネットワーク,脳波,共感覚,1/f揺らぎ
  15. 1/7(金) 自由制作日
  16. 1/14(金) 休講：センター試験準備日
  17. 1/21(金) 小テスト

2008年スケジュール

担当
久原，小川
  1. 9/22(月)生物と情報とアート，セルオートマトン
  2. 9/29(月) セルオートマトンを使った音楽生成
    • Minutes Paper 「セルオートマトンを使ったアートの例をしらべ、リンクをはり、簡単な説明をしてください。」
  3. 10/6(月) アロマアート,ヒーリングアート
    • Minutes Paper 「好きな香りは何ですか？」
    • 10/13(月) 体育の日
  4. 10/16(木) 月曜授業振替日アロマアート、共感覚、1/f揺らぎ
    • Minutes Paper 「自分にとって癒される音は？」
  5. 10/20(月) C#によるオブジェクト指向プログラミング(C#実習)
    • Minutes Paper 「オブジェクト指向とは？」
    • 10/27(月) 工芸祭片付け日
    • 11/3(月) 文化の日
  6. 11/5(水) 月曜授業振替日 幾何学図形の描画(C#実習)
    • Minutes Paper 「プログラミング言語につきもののif文とは？」
  7. 11/10(月) 幾何学図形の描画(C#実習)
    • Minutes Paper 「プログラミング言語につきもののforループとは？」
  8. 11/17(月) 三角関数を使った描画、1次元セルオートマトンによる描画(C#実習)
    • Minutes Paper 「三角関数はアーティストにとって使える道具であるといえるのはなぜか？」
    • 11/24(月) 振替休日
  9. 12/1(月) 課題提出(C#実習)
  10. 12/8(月) フラクタル、再起呼出しによる自己相似形(C#実習)
    • Minutes Paper 「身近な所に見られる再帰呼出しの例」
  11. 12/15(月) 複素平面フラクタル,ニューラルネットワーク,遺伝的アルゴリズム
    • Minutes Paper 「自分の好きな生物とその品種は？」
  12. 12/22(月) 小テスト

2007年スケジュール

担当
久原，町田
  1. --- 9/17(月) 敬老の日
  2. --- 9/24(月) 秋分の日
  3. 10/1(月) 生物と情報とアート，セルオートマトン
  4. --- 10/8(月) 体育の日
  5. 10/15(月) アロマアート
  6. 10/22(月) ヒーリングアート
  7. --- 10/29(月) 工芸祭片付け日
  8. 11/5(月) フラクタル
  9. 11/12(月) C#プログラミングの基礎(PC実習)
  10. 11/19(月) 幾何学図形の描画(C#実習)
  11. 11/26(月) 幾何学図形の描画(C#実習)
  12. 12/3(月) 再起呼出しによる自己相似形の描画(C#実習)
  13. 12/10(月) 共感覚実験調査，複素平面フラクタル
  14. 12/17(月) Neural Networks, Genetic Algorithm
  15. 12/19(水) 月曜授業振替日 課題提出日
  16. 12/20(木) 月曜授業振替日 小テスト

課題

2008年度

締切は、いずれの課題も12/22(月)18:10です。
  1. 幾何学模様画像
    • C#を使用して，幾何学模様画像を描くプログラムを作成しなさい。
    • 提出方法:プロジェクトフォルダーを以下の通り，提出用フォルダーに提出してください。
      • プロジェクトフォルダー名：学籍番号　例 0824000
      • 提出用フォルダー：Weekly内の以下のフォルダーに提出してください。
        • MA表現学科の学生：「W:\art\media\kuhara\」
        • 写真学科の学生：「W:\art\pht\kuhara\」
        • 映像学科の学生：「W:\art\manga\kuhara\」
  1. 複素平面フラクタル画像
    • 提出先 サイボウズ提出スレッド
    • 他学科の学生は、kuha@media.t-kougei.ac.jpへ添付して送ってください。必ず学科、学籍番号、氏名を明記すること。

2007年度

締切は、いずれの課題も12/19(水)です。
  1. 自己相似系画像
    • C#の再帰的呼び出しを使用して，自己相似系画像を描くプログラムを作成しなさい。
    • 提出方法:プロジェクトフォルダーを以下の通り，提出用フォルダーに提出してください。
      • プロジェクトフォルダー名：rc学籍番号　例 rc0724000
      • 提出用フォルダー：Weekly内の以下のフォルダーに提出してください。
        • MA表現学科の学生：「W:\art\media\kuhara\再帰的呼出プログラム課題」
        • 写真学科の学生：「W:\art\pht\kuhara\再帰的呼出プログラム課題」
        • 映像学科の学生：「W:\art\img\kuhara\再帰的呼出プログラム課題」
        • デザイン学科の学生：「W:\art\dsn\kuhara\再帰的呼出プログラム課題」
  2. 複素平面フラクタル画像
    • 複複素平面フラクタル図形描画ソフトウェア for Windowsを使用して，フラクタル画像を作成しなさい。
    • 画像は、ペイントなどのソフトでJPG形式に変換してください。
    • 提出先:フラクタル画像BBS:書込み内容は以下の通り
      • お名前：学籍番号と氏名
      • タイトル：複素平面フラクタル
      • メッセージ：
        • テーマ：作成した画像のテーマを書いてください。
        • 数値：Real Scale, Image Scale, A real, A image, Resolutionの値を例にならって書いてください。
        • コメント：自己評価などを書いてください。
    • 投稿記事を修正したり，削除したりするには，末尾にあるフォームに記事番号(NO)とパスワード(PASS)を入れて「送信」ボタンを押してください。PASSは記事投稿時に指定したパスワードです。投稿時にパスワードを省略した場合はPASSなしで修正・削除ができます。

メッセージ記入例 

テーマ：マゼンタな太陽
数値：
Real Scale:-0.3 to 0.3
Image Scale:-0.3 to 0.3
A real -1.24
A image 0.075
Resolution 250
コメント：自己評価などを書いてください。

生物と情報とアート

複雑系

セルオートマトン

ライフゲーム

ライフゲームの例 / ライフゲーム入門 / セルオートマトン・ギャラリー /

セルオートマトン音楽

WolframTones/ CAMUS/ Glitch DS/

ギャラリー

Modern Cellular Automata/ CArt gallery/ Cellular Automata Art/ ASCII Art Cell Automaton/

参考

ワイヤワールド /

人工生命

ラングトンのアリ / ラングトンのループ / 自己増殖ループ


C#プログラミング

Visual Studio C#を使用した描画プログラムの作成

プロパティの変更

ラベルの変更 
label1.Text = "おはよう";
label1.BackColor = Color.FromArgb(100,0,255,0);

乱数の使用

サイコロ 
Random saikoro = new Random();
label2.Text = saikoro.Next(1, 7).ToString();

Timerの使用

ルーレット
  • Timerのスタートとストップのトグルボタン 
if (timer1.Enabled == true)
{
  timer1.Stop();
}
else
{
  timer1.Start();
}
  • timer1_Tick()メソッドの処理。Interval時間間隔ごとにテキストボックスから得た数字を最大値として乱数を発生させる。 
Random roulette = new Random();
int kazu_max = int.Parse(textBox1.Text);
label2.Text = roulette.Next(1, kazu_max).ToString();


幾何学模様描画例

描画例のソース

exeプログラム例 直線，矩形，円弧，多角形，曲線など

線の描画

  • pictureboxを作成
  • Graphic gの作成
  • Penの作成
  • g.Draw系のメソッドで線を描画

以下のライブラリーをインポートしておく。 

using System.Drawing.Drawing2D;

Graphics g = pictureBox1.CreateGraphics();//pictureBox1に描画するオブジェクトを作成

g.DrawLine(Pens.Black, 0, 0, pictureBox1.Width, 0);  // 普通の直線
Pen boldPen = new Pen(Color.Black, 5);  // 太い線
g.DrawLine(boldPen, 0, 30, pictureBox1.Width, 30);

g.DrawRectangle(Pens.Black, 0, 0, 100, 100);   // 四角形を描画する
g.FillRectangle(Brushes.Red, 50, 50, 100, 100);   // 塗り潰しの四角形を描画する

g.DrawEllipse(Pens.Black, 0, 0, 100, 100);   // 円を描画する
g.DrawEllipse(Pens.Black, 0, 0, 200, 100);    // 楕円を描画する
g.DrawArc(Pens.Black, 200, 0, 100, 100, 10, 275);  // 円弧を描画する
g.DrawPie(Pens.Black, 300, 0, 100, 100, 10, 275);  // 扇形を描画する
g.FillEllipse(Brushes.Red, 50, 50, 100, 100);  // 塗り潰した円を描画する

Point[] points = new Point[4]; // 開いた多角形を描画する
points[0] = new Point(50, 0);
points[1] = new Point(100, 50);
points[2] = new Point(50, 100);
points[3] = new Point(0, 50);
g.DrawLines(Pens.Black, points);

points[0] = new Point(100, 0);  // 閉じた多角形を描画する
points[1] = new Point(150, 50);
points[2] = new Point(100, 100);
points[3] = new Point(50, 50);
g.DrawPolygon(Pens.Red, points);

points[0] = new Point(0, 0);
points[1] = new Point(100, 200);
points[2] = new Point(200, 0);
points[3] = new Point(300, 200);
g.DrawLines(Pens.Black, points);

// 曲線を描画する
g.DrawBeziers(Pens.Black, points);  //ヴェジェ

g.DrawCurve(Pens.Red, points);  //スプライン
g.DrawCurve(Pens.Red, points, 0F);
g.DrawCurve(Pens.Red, points, 0.5F);
g.DrawCurve(Pens.Red, points, 1F);
g.DrawCurve(Pens.Red, points, 1.5F);
g.DrawCurve(Pens.Red, points, 2F);

描画領域のクリア 

g.Clear(Color.White); //描画領域をクリア

グラデーション 

Graphics g = pictureBox1.CreateGraphics();
// グラデーションのペンを作成
Brush br = new LinearGradientBrush(new Point(0, 0), new Point(0, pictureBox1.Height), Color.Green, Color.White);
// グラデーションで塗り潰し
g.FillRectangle(br, 0, 0, pictureBox1.Width, pictureBox1.Height);

マウスムーブを使った描画

プロパティウィンドウにイベントのリストを表示させ、MouseMoveイベントをダブルクリックすると、MouseMoveのメソッドが自動生成されます。 

private void pictureBox1_MouseMove(object sender, MouseEventArgs e)
{
  Graphics g = pictureBox1.CreateGraphics();
  Pen pen = new Pen(Color.Black);
  Random rndcolor = new Random();
  //描画色の決定
  int aa = rndcolor.Next(0, 256);
  int rr = rndcolor.Next(0, 256);
  int gg = 255 - e.X * 255 / pictureBox1.Width;
  int bb = e.Y * 255 / pictureBox1.Height;
  pen.Color = Color.FromArgb(aa, rr, gg, bb);
  // マウス位置へ直線を描画する
  g.DrawLine(pen, 0, 0, e.X, e.Y);
  g.DrawLine(pen, 0, pictureBox1.Height, e.X, e.Y);
  g.DrawLine(pen, pictureBox1.Width, 0, e.X, e.Y);
  g.DrawLine(pen, pictureBox1.Width, pictureBox1.Height, e.X, e.Y);
  label3.Text = e.X.ToString();
  label4.Text = e.Y.ToString();
}

forループを使った描画 

  Graphics g = pictureBox1.CreateGraphics();

// 直線をループで描画する
  Pen pen = new Pen(Color.Black);
  Random rnd = new Random();
  for (int i = 0; i < pictureBox1.Width; i++)
  {
    int aa = rnd.Next(0, 256);
    int rr = rnd.Next(0, 256);
    int gg = rnd.Next(0, 256);
    int bb = rnd.Next(0, 256);
    pen.Color = Color.FromArgb(aa, rr, gg, bb);
    g.DrawLine(pen, pictureBox1.Width / 2, 0, i, pictureBox1.Height);
  }

// 点をループで描画する
  SolidBrush brush = new SolidBrush(Color.Black);
  Random rnd = new Random();
  int imax = 10000;
  for (int i = 0; i < imax; i++)
  {
    int aa = rnd.Next(0, 256);
    int rr = rnd.Next(0, 256);
    int gg = rnd.Next(0, 256);
    int bb = rnd.Next(0, 256);
    int xx = rnd.Next(0, pictureBox1.Width);
    int yy = rnd.Next(0, pictureBox1.Height);
    pen.Color = Color.FromArgb(aa, rr, gg, bb);
    brush.Color = Color.FromArgb(aa, rr, gg, bb);
    g.DrawRectangle(pen, xx, yy, 5, 5);
    g.FillRectangle(brush, xx, yy, 5, 5);
  }

// 円をループで描画する
    double pi = 3.14159;
   int x3 = pictureBox1.Width / 2;
   int y3 = pictureBox1.Height / 2;
   int r1 = 100, r2 = 50;
   int kkizami = 100;
   int shukai = 1;
   int n = 5;
   for (int i = 0; i < kkizami * shukai; i++)
   {
     double k = 2 * pi / kkizami * i;
     double x = x3 + r1 * Math.Cos(k);
     double y = y3 - r1 * Math.Sin(k);
     g.DrawEllipse(pen, (int)x - r2, (int)y - r2, 2 * r2, 2 * r2);
   }

アルキメデスの渦巻き 

Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Black);
double pi = 3.14159;
int x3 = pictureBox1.Width / 2;
int y3 = pictureBox1.Height / 2;
double r1;
int kkizami = 1000;
int shukai = 100;
double n = 2;
double k,x=0,y=0,nx=0,ny=0;
nx = x3; ny = y3;
for (int i = 0; i < kkizami * shukai; i++)
{
  k = 2 * pi / kkizami * i;
  r1 = n * k;
  x = nx;
  y = ny;
  nx = x3 + r1 * Math.Cos(k);
  ny = y3 - r1 * Math.Sin(k);
  g.DrawLine(pen, (int)x, (int)y, (int)nx, (int)ny);
}

フェルマーの渦巻き 

Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Black);
double pi = 3.14159;
int x3 = pictureBox1.Width / 2;
int y3 = pictureBox1.Height / 2;
double r1;
int kkizami = 100;
int shukai = 100;
double n = 10;
double k, x = 0, y = 0, nx = 0, ny = 0;
nx = x3; ny = y3;
for (int i = 0; i < kkizami * shukai; i++)
{
  k = 2 * pi / kkizami * i;
  r1 = n * Math.Sqrt(k);
  x = nx;
  y = ny;
  nx = x3 + r1 * Math.Cos(k);
  ny = y3 - r1 * Math.Sin(k);
  g.DrawLine(pen, (int)x, (int)y, (int)nx, (int)ny);
}

正葉曲線：単 

Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Black);
double pi = 3.14159;
int x3 = pictureBox1.Width / 2;
int y3 = pictureBox1.Height / 2;
double r1;
int kkizami = 1000;
int shukai = 1;
double n = 5,m=100;
double k, x = 0, y = 0, nx = 0, ny = 0;
nx = x3; ny = y3;
for (int i = 0; i < kkizami * shukai; i++)
{
  k = 2 * pi / kkizami * i;
  r1 = m * Math.Abs(Math.Sin(n * k));
  x = nx;
  y = ny;
  nx = x3 + r1 * Math.Cos(k);
  ny = y3 - r1 * Math.Sin(k);
  g.DrawLine(pen, (int)x, (int)y, (int)nx, (int)ny);
}

正葉曲線：複 

Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Black);
double pi = 3.14159;
int x3 = pictureBox1.Width / 2;
int y3 = pictureBox1.Height / 2;
double r1;
int kkizami = 1000;
int shukai = 1;
double n = 5, m = 20;
double k, x = 0, y = 0, nx = 0, ny = 0;
nx = x3; ny = y3;
for (int i = 0; i < kkizami * shukai; i++)
{
  k = 2 * pi / kkizami * i;
  r1 = m * Math.Abs( 7* Math.Sin(n * k) + 1 * Math.Sin(3 * n * k) + 1 * Math.Sin(5 * n * k ));
  x = nx;
  y = ny;
  nx = x3 + r1 * Math.Cos(k);
  ny = y3 - r1 * Math.Sin(k);
  g.DrawLine(pen, (int)x, (int)y, (int)nx, (int)ny);
}

外サイクロイド 

Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Black);
double pi = 3.14159;
int x3 = pictureBox1.Width / 2;
int y3 = pictureBox1.Height / 2;
double r1;
int kkizami = 100;
int shukai = 50;
double a = 100, b = 65;
double k, x = 0, y = 0, nx = 0, ny = 0;
nx = x3 + a; ny = y3;
for (int i = 0; i < kkizami * shukai; i++)
{
  k = 2 * pi / kkizami * i;
  x = nx; y = ny;
  nx = x3 + ((a + b) * Math.Cos(k) - b * Math.Cos((a + b) / b * k));
  ny = y3 - ((a + b) * Math.Sin(k) - b * Math.Sin((a + b) / b * k));
  g.DrawLine(pen, (int)x, (int)y, (int)nx, (int)ny);
}

内サイクロイド 

Graphics g = pictureBox1.CreateGraphics();
Pen pen = new Pen(Color.Black);
double pi = 3.14159;
int x3 = pictureBox1.Width / 2;
int y3 = pictureBox1.Height / 2;
double r1;
int kkizami = 100;
int shukai = 50;
double a = 100, b = 23;
double k, x = 0, y = 0, nx = 0, ny = 0;
for (int i = 0; i < kkizami * shukai; i++)
{
  k = 2 * pi / kkizami * i;
  if (i == 0)
  {
     x = x3 + ((a - b) * Math.Cos(k) + b * Math.Cos((a - b) / b * k));
     y = y3 - ((a - b) * Math.Sin(k) - b * Math.Sin((a - b) / b * k));
  }
  else
  {
     x = nx;
     y = ny;
  }
     nx = x3 + ((a - b) * Math.Cos(k) + b * Math.Cos((a - b) * k / b));
     ny = y3 - ((a - b) * Math.Sin(k) - b * Math.Sin((a - b) * k / b));
     g.DrawLine(pen, (int)x, (int)y, (int)nx, (int)ny);
  }
}


セルオートマトン例

1次元セルオートマトン

実行例 

// グラフィック，描画ブラシ，乱数の準備
Graphics g = pictureBox1.CreateGraphics();
SolidBrush brush = new SolidBrush(Color.Black);
Random rnd = new Random();

// セルの状態格納用の2次元整数型配列を用意
int ookisa = 100;//　配列の大きさ
int[ , ] cell = new int[ookisa, ookisa];

//セルの初期状態
for (int j = 0; j < ookisa; j++)
{
  cell[0, j] = rnd.Next(0, 0);
}
cell[0, ookisa / 2] = 128;

//セルの状態遷移則
for (int i = 1; i < ookisa; i++)
{
  for (int j = 1; j < ookisa - 1; j++)
  {
     cell[i, j] = (cell[i - 1, j - 1] + cell[i - 1, j + 1]) % 256;
  }
}

//セルの描画
int pixsz = 5;
for (int i=0; i < ookisa; i++){
  for (int j=0; j < ookisa; j++)
  {
    brush.Color = Color.FromArgb(255, cell[i, j], 0, 0);
    g.FillRectangle(brush, j * pixsz, i * pixsz, pixsz, pixsz);
  }
}

変化形 

//セルの初期状態
for (int j = 0; j < ookisa; j++)
{
   cell[0, j] = rnd.Next(0, 0) ;
}
cell[0, ookisa / 2] = 7;
cell[0, ookisa / 3] = 6;
cell[0, ookisa / 4] = 3;
cell[0, ookisa / 3 * 2] = 70;

//セルの状態遷移則
for (int i = 1; i < ookisa; i++)
{
  for (int j = 1; j < ookisa - 1; j++)
  {
     cell[i, j] = (cell[i - 1, j - 1] + cell[i - 1, j + 1] + cell[i - 1, j] ) % 256;
  }
}

//セルの描画
int pixsz = 5;
for (int i=0; i < ookisa; i++)
{
  for (int j=0; j < ookisa; j++)
  {
     brush.Color = Color.FromArgb(255, cell[i, j], cell[j, i], 0);
     g.FillRectangle(brush, j * pixsz, i * pixsz, pixsz, pixsz);
  }
}

フラクタル

古代ギリシャからあるユークリッド幾何学と20世紀のフラクタル幾何学の比較

考察
古代エジプト人は3:4:5の辺を持つ三角形で直角が得られることを知っていた．ピラミッドなどの巨大建造物．
三平方の定理を発見したピタゴラスはどこがすごいか？
フラクタル図形

配布資料PDF / フラクタル図形の例

フラクタル日除け

自己相似系

  • 再帰的呼出しによる樹木の描画（PC実習）配布資料
    • 再帰的( recursive )呼び出しとは，サブルーチンや関数が，自分自身を呼び出すことをいう。樹木は，枝の１つを取り出して拡大しても，元の枝と同じ形（相似形）をしている。これは，同じサブルーチンで枝を描画しているからである。
  • 再帰的呼出し的なCollaborate Flash Animation：zoomquilt (swf)
  • 例：実行ファイル，ソース，Taneクラス

C#による実装

新しいクラスの定義

  • 「プロジェクト」メニューから「クラスの追加」で新しいクラス名を入力する。クラスの定義の中にメソッドを記述する。
  • 注意 
using System.Drawing;

をTane.csの冒頭に追加

樹木の描画

Bintree.jpg Bintree2.JPG

Taneクラスのメソッド

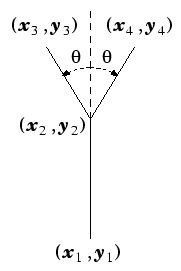
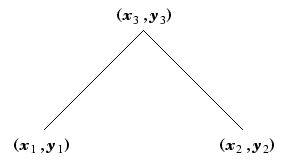
線分(x1,y1)-(x2,y2)が与えられたら、(x2,y2)の先端に(x3,y3), (x4,y4)を取り、線分(x2,y2)-(x3,y3)と線分(x2,y2)-(x4,y4)を描画する。 

    class Tane
    {
        public void Eda(int n, double x1, double y1, double x2, double y2, double angle, Graphics g, Pen pen)
        {
            double x3, y3, x4, y4;
            double s = Math.Sin(angle * Math.PI / 180.0);
            double c = Math.Cos(angle * Math.PI / 180.0);
            double dx = 0.7 * (x2 - x1);
            double dy = 0.7 * (y2 - y1);

            if (n > 0)
            {
                x3 = x2 + dx * c - dy * s;
                y3 = y2 + dx * s + dy * c;
                x4 = x2 + dx * c + dy * s;
                y4 = y2 - dx * s + dy * c;
                // 枝を描画する
                g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
                g.DrawLine(pen, (float)x2, (float)y2, (float)x3, (float)y3);
                g.DrawLine(pen, (float)x2, (float)y2, (float)x4, (float)y4);
                //子の再起呼び出し
                Eda(n - 1, x2, y2, x3, y3, angle, g, pen);
                Eda(n - 1, x2, y2, x4, y4, angle, g, pen);
            }
        }
    }
樹木描画ボタンクリックの中身 
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 2);
            Tane tane = new Tane();

            int n = 10;  //枝の世代数
            double x0 = pictureBox1.Width / 2; //開始位置 x座標
            double y0 = pictureBox1.Height; //開始位置 y座標
            double x1 = pictureBox1.Width / 2; //開始位置 x座標
            double y1 = pictureBox1.Height * 0.8; //開始位置 y座標
            double angle = 30.0; //子供の枝の角度の差分
            tane.Eda(n, x0, y0, x1, y1, angle, g, pen);

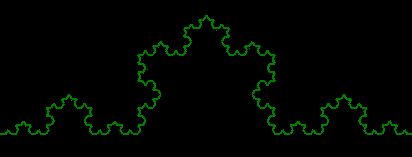
コッホ図形の描画

Koch.jpg Koch2.jpg


Taneクラスのメソッド 
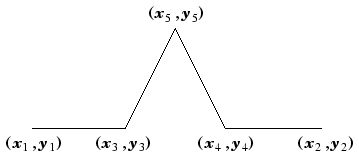
        public void Koch(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
        {
            double x3, y3, x4, y4, x5, y5;
            double s = Math.Sin(Math.PI / 3.0);
            double c = Math.Cos(Math.PI / 3.0);

            if (n > 0)
            {
                x3 = (2 * x1 + x2) / 3.0;
                y3 = (2 * y1 + y2) / 3.0;
                x4 = (x1 + 2 * x2) / 3.0;
                y4 = (y1 + 2 * y2) / 3.0;
                x5 = x3 + (x4 - x3) * c + (y4 - y3) * s;
                y5 = y3 - (x4 - x3) * s + (y4 - y3) * c;
                // ジェネレータを描画する
                pen.Color = Color.Black;
                g.DrawLine(pen, (float)x3, (float)y3, (float)x4, (float)y4);
                pen.Color = Color.Green;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
                g.DrawLine(pen, (float)x3, (float)y3, (float)x5, (float)y5);
                g.DrawLine(pen, (float)x5, (float)y5, (float)x4, (float)y4);
                g.DrawLine(pen, (float)x4, (float)y4, (float)x2, (float)y2);
                // 子の再起呼び出し
                Koch(n - 1, x1, y1, x3, y3, g, pen);
                Koch(n - 1, x3, y3, x5, y5, g, pen);
                Koch(n - 1, x5, y5, x4, y4, g, pen);
                Koch(n - 1, x4, y4, x2, y2, g, pen);
            }
        }
コッホ図形描画ボタンクリックの中身 
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 2);
            Tane tane = new Tane();

            // マウス位置へ直線を描画する
            int n = 4;  //子の世代数
            double x0 = 0; //開始位置 x座標
            double y0 = pictureBox1.Height * 0.6 ; //開始位置 y座標
            double x1 = pictureBox1.Width; //終了位置 x座標
            double y1 = pictureBox1.Height * 0.6; //終了位置 y座標
            tane.Koch(n, x0, y0, x1, y1, g, pen);

ドラゴン図形の描画

Dragon.jpg Dragon2.jpg

Taneクラスのメソッド 
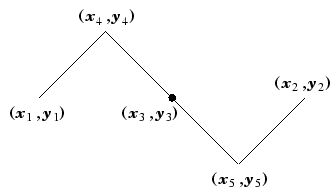
        public void Dragon(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
        {
            double x3, y3, x4, y4, x5, y5;

            if (n > 0)
            {
                x3 = 0.5 * ( x1 + x2);
                y3 = 0.5 * ( y1 + y2);
                x4 = 0.5 * (x1 + x3 - y1 + y3);
                y4 = 0.5 * (x1 - x3 + y1 + y3);
                x5 = 0.5 * (x2 + x3 - y2 + y3);
                y5 = 0.5 * (x2 - x3 + y2 + y3);

                // 枝を描画する
                pen.Color = Color.Black;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
                g.DrawLine(pen, (float)x3, (float)y3, (float)x2, (float)y2);
                pen.Color = Color.Green;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x4, (float)y4);
                g.DrawLine(pen, (float)x4, (float)y4, (float)x3, (float)y3);
                g.DrawLine(pen, (float)x3, (float)y3, (float)x5, (float)y5);
                g.DrawLine(pen, (float)x5, (float)y5, (float)x2, (float)y2);
                Dragon(n - 1, x1, y1, x4, y4, g, pen);
                Dragon(n - 1, x4, y4, x3, y3, g, pen);
                Dragon(n - 1, x3, y3, x5, y5, g, pen);
                Dragon(n - 1, x5, y5, x2, y2, g, pen);
            }
        }
ドラゴン図形描画ボタンクリックの中身 
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 2);
            Tane tane = new Tane();

            // マウス位置へ直線を描画する
            int n = 7;  //子の世代数
            double x0 = pictureBox1.Width * 0.1; //開始位置 x座標
            double y0 = pictureBox1.Height * 0.5; //開始位置 y座標
            double x1 = pictureBox1.Width * 0.9; //終了位置 x座標
            double y1 = pictureBox1.Height * 0.5; //終了位置 y座標
            tane.Dragon(n, x0, y0, x1, y1, g, pen);

シダ葉の描画

Sida2.JPG

Taneクラスのメソッド 
        public void Fern(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
        {
            double x3, y3, x4, y4, x5, y5;

            if (n > 0)
            {
                x3 = ( x1 + x2 ) / 2.0;
                y3 = ( y1 + y2 ) / 2.0;
                x4 = ( x1 + x3 - y1 + y3) / 2.0;
                y4 = ( x1 - x3 + y1 + y3) / 2.0;
                x5 = ( x2 + x3 - y2 + y3) / 2.0;
                y5 = ( x2 - x3 + y2 + y3) / 2.0;
                // 枝を描画する
                pen.Color = Color.Green;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
                g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
                g.DrawLine(pen, (float)x3, (float)y3, (float)x5, (float)y5);
                Fern(n - 1, x1, y1, x4, y4, g, pen);
                Fern(n - 1, x1, y1, x3, y3, g, pen);
                Fern(n - 1, x3, y3, x2, y2, g, pen);
                Fern(n - 1, x3, y3, x5, y5, g, pen);
            }
        }
シダ葉描画ボタンクリックの中身 
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 2);
            Tane tane = new Tane();

            int n = 7;  //子の世代数
            double x0 = pictureBox1.Width * 0.1; //開始位置 x座標
            double y0 = pictureBox1.Height * 0.5; //開始位置 y座標
            double x1 = pictureBox1.Width * 0.9; //終了位置 x座標
            double y1 = pictureBox1.Height * 0.5; //終了位置 y座標
            tane.Fern(n, x0, y0, x1, y1, g, pen);

Cカーブの描画

Ccurve.jpg Ccurve2.jpg

Taneクラスのメソッド 
        public void Ccurve(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
        {
            double x3, y3;

            if (n > 0)
            {
                x3 = 0.5 * (x1 + x2 - y1 + y2);
                y3 = 0.5 * (x1 - x2 + y1 + y2);
                // 枝を描画する
                pen.Color = Color.Black;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
                pen.Color = Color.Green;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x3, (float)y3);
                g.DrawLine(pen, (float)x3, (float)y3, (float)x2, (float)y2);
                Ccurve(n - 1, x1, y1, x3, y3, g, pen);
                Ccurve(n - 1, x3, y3, x2, y2, g, pen);
            }
        }
Cカーブ画ボタンクリックの中身 
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 2);
            Tane tane = new Tane();

            int n = 12;  //子の世代数
            double x0 = pictureBox1.Width * 0.25; //開始位置 x座標
            double y0 = pictureBox1.Height * 0.75; //開始位置 y座標
            double x1 = pictureBox1.Width * 0.75; //終了位置 x座標
            double y1 = pictureBox1.Height * 0.75; //終了位置 y座標
            tane.Ccurve(n, x0, y0, x1, y1, g, pen);

内分点と回転によるカスタムジェネレータの描画

Gene01.JPG Gene012.JPG

Taneクラスのメソッド 
        public void Gene01(int n, double x1, double y1, double x2, double y2, Graphics g, Pen pen)
        {
            double x3, y3, x4, y4;
            double p = 2.0;
            double q = 3.0;
            double th = -30.0;
            double s = Math.Sin(th * Math.PI / 180.0);
            double c = Math.Cos(th * Math.PI / 180.0);

            if (n > 0)
            {
                x3 = (q * x1 + p * x2) / (p + q);
                y3 = (q * y1 + p * y2) / (p + q);
                x4 = x1 + (x3 - x1) * c - (y3 - y1) * s;
                y4 = y1 + (x3 - x1) * s + (y3 - y1) * c;
                pen.Color = Color.Yellow;
                g.DrawLine(pen, (float)x1, (float)y1, (float)x2, (float)y2);
                g.DrawLine(pen, (float)x1, (float)y1, (float)x4, (float)y4);
                Gene01(n - 1, x1, y1, x3, y3, g, pen);
                Gene01(n - 1, x1, y1, x4, y4, g, pen);
                Gene01(n - 1, x3, y3, x2, y2, g, pen);
            }
        }
カスタムジェネレータ描画ボタンクリックの中身 
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 2);
            Tane tane = new Tane();

            int n = 7;  //子の世代数
            double x0 = pictureBox1.Width * 0.1; //開始位置 x座標
            double y0 = pictureBox1.Height * 0.5; //開始位置 y座標
            double x1 = pictureBox1.Width * 0.9; //終了位置 x座標
            double y1 = pictureBox1.Height * 0.5; //終了位置 y座標
            tane.Gene01(n, x0, y0, x1, y1, g, pen);

タイマーを使用した樹木のアニメーション 

        private void button3_Click(object sender, EventArgs e)
        {
            timer1.Enabled = true;
            timer1.Start();
        }

        private void button4_Click(object sender, EventArgs e)
        {
            timer1.Stop();
            timer1.Enabled = false;
        }


        public int cnt; //タイマー用カウンタ
        private void timer1_Tick(object sender, EventArgs e)
        {
            Graphics g = pictureBox1.CreateGraphics();
            Pen pen = new Pen(Color.Green, 1);
            Tane tane = new Tane();

            g.Clear(Color.Black);

            cnt++;  //タイマー用カウンタのカウントアップ
            int n = 10;  //枝の世代数
            double x0 = pictureBox1.Width / 2; //開始位置 x座標
            double y0 = pictureBox1.Height; //開始位置 y座標
            double x1 = pictureBox1.Width / 2; //開始位置 x座標
            double y1 = pictureBox1.Height * 0.9 - cnt * 2; //開始位置 y座標
            double angle = 30.0; //子供の枝の角度の変化の差分
            double a_rate = angle + cnt * 2;
            tane.Eda(n, x0, y0, x1, y1, a_rate, g, pen);
        }

複素平面フラクタル

Powers of Ten

人間の感覚

アロマアート

嗅覚を利用したアート

かんたん掲示板に「香りの特徴」を書いてみよう。

共感覚

ヒーリングアート

リラックスとリフレッシュ
リラックス時には副交感神経が優勢に，興奮状態にある場合は、交感神経が優勢になる。
リラックス時にはアルファ波が出る？
1/f揺らぎ
  • ホワイトノイズ、サイン波、ピンクノイズ(1/f揺らぎ)
  • 自然界の音を使用した楽曲 URL
  • スペクトル
    • EQ(イコライザ)によって，音のスペクトルを加工する。
    • スペクトルとは周波数構成のこと。ピッチ感のある音は，ピークとなる基本周波数を中心として複数の倍音成分から構成される。
      • SoundEngineやAudacityでsin波などを生成し，周波数構成を観察。sin波は基本周波数１つのみ。ノコギリ波はsin波の倍数の無限級数。ホワイトノイズはランダムな周波数構成。
      • 人のボーカル，楽器の音，車のエンジン音のスペクトルを比較してみる。
子守唄
  • 子守唄の特徴、西洋の子守唄、日本の子守唄
  • 子守唄自動作曲プログラム(Max/MSP)PDF
  • 生理食塩水内レコーディング竹田の子守唄
生物的なシステム，生物の癒し効果

flash effects / Levitated the Exploration of Computation / sodaplay/ Vector Park / リヴリー・アイランド / エレクトロプランクトン / たまごっちプラス / メンタルコミットロボアザラシ型「パロ」 / 猫型コミュニケーションロボット「ネコロ」 / nintendogs / What is TRUTH? /


脳

脳波，脳電図(electroencephalogram EEG)
大脳皮質のニューロンの膨大な数のシナプス結合における電位（シナプス後電位）の集合と考えられている。
通常は，空間的および時間的分散性のために一定の形状の波形にはならない。しかし，大脳皮質の活性度が低下した時にはある程度の同期性がみられ，その代表的な状態が睡眠時の脳波である。
開眼時，脳の神経細胞があちこちで活発に作動していると，シナプス電位は同期が取れずに，脳波はランダムなになり，特定の周波数は測定されない。
  • デルタ波(δ波)：1～3Hz ぐっすり睡眠．昏睡．
  • シータ波(θ波)：4～7Hz うたたうね．ぼんやり．
  • アルファ波(α波)：8～13Hz 覚醒，安静，閉眼時。リラックス。
  • ベータ波(β波)：14～30Hz 開眼時，五感が働いている状態。活発な思考。
  • ガンマ波(γ波)：30～64Hz 高次精神活動に関連（？）
  • オメガ波(ω波)：64～128Hz（？）
  • ロー波(ρ波)：128-512Hz （？）
  • シグマ波(σ波)：512-1024Hz （？）
  • アーティファクト：ノイズ（雑音）。まばたき，眼球運動，電極の接着不良など脳と無関係のものが要因。

バイノーラルビート

周波数追従反応

脳磁図，生物フォトン，心電図，筋電図，眼電図。

ニューロコミュニケーター

Neural Networks

  • 神経回路モデル（PPT）
  • 神経細胞の写真，構成図[ 1 | 2 | 3 ]
  • ニューラルネットワーク入門
  • Perceptron,
  • Back Propagation
  • Hopfield Network
  • 自己組織化ネットワーク
  • 脳の潜在能力
    • 天文学者カール・セーガン「人間の脳はおよそ2,000万冊，すなわち世界最大の図書館に収められているのと同じ数の本を満たすほどの情報を収納することができる」
    • 神経科学者「人は平均寿命の間に脳の潜在能力の0.01％（0.0001）しか使っていない」

Genetic Algorithm

配布資料PDF

小テスト

  • 場所　いつものPC演習室
  • 出題　配布資料などから出題されます。ノート，配布資料などを復習しておいてください。問題の形式は，選択式です。
  • 注意事項
    • 座席は自由ですが，隣の座席を１つ空けて座ってください。
    • 持ち込みは不可です。机の上には一切，何も置かないで下さい。
    • PC上のソフトはブラウザだけ起動してください。他のアプリケーションはすべて終了させてください。

小テスト

「http://w3.kuhalabo.net/wiki/index.php?title=%E7%94%9F%E5%91%BD%E6%83%85%E5%A0%B1%E3%82%A2%E3%83%BC%E3%83%88%E8%AB%96&oldid=276」から取得
個人用ツール
名前空間

変種
操作
案内
ツールボックス